有哪些题目看着简单,但实际上做起来非常「折磨人」?

提名一个高中教材上就有,但是让你自己想能让你想破头都未必给得出的一个证明:纯几何法证明圆锥的截口曲线是椭圆、双曲线或者抛物线。
如果这个问题让你用圆锥面的一般方程来做(至于什么是圆锥面的一般方程,看我二次型的内容),那么没有任何难度(毕竟,形如
的方程代表的曲线类型还是比较容易求得的);而我接下来贴出来的,就是纯几何法的证明过程。
圆和两条直线就太简单了,但是我还是会贴出来,先卖个关子。椭圆的情况是怎么样的呢?
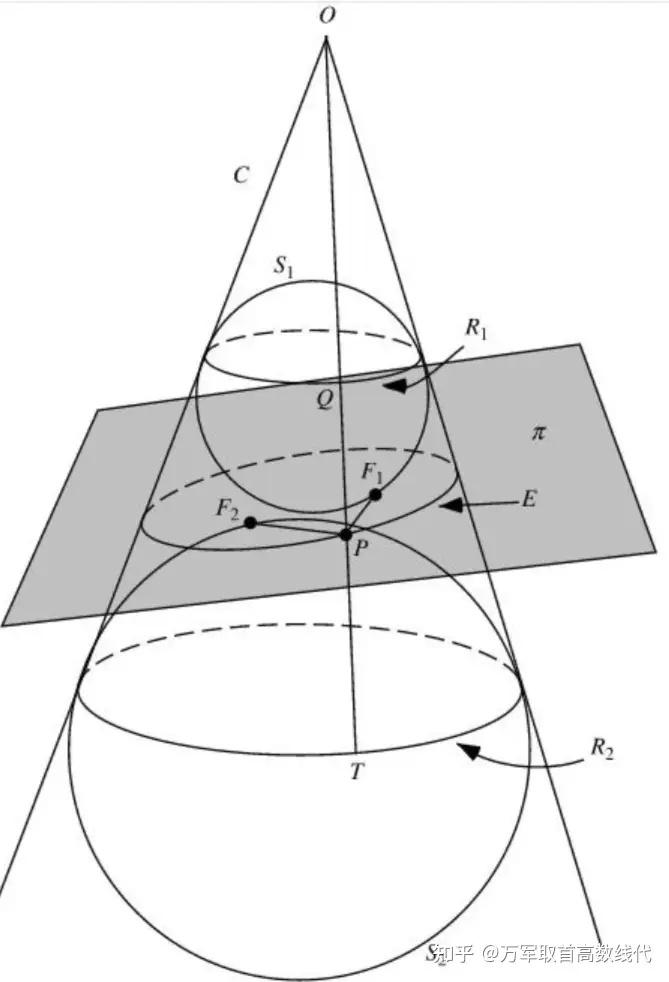
比如,这里我们就可以用 Dandelin 双球模型来证明,图中圆锥和平面的交线是圆。假设这两个球与圆锥和平面都相切(也就是说,这两个球一方面,球心位于圆锥的轴线上,且它们的主视图是与圆锥的主视图相切的圆;另一方面,和平面相切),那么根据切线长定理,我们能够得到
为定值。这样,我们就知道了这个椭圆的焦点,就是平面和两个球的切点;而长轴长就是
的长度。
当然,在圆柱中,我们也可以通过构造这样的双球模型,来证明截口曲线是椭圆。
同样,这张图,能够证明圆锥曲线可以是抛物线。
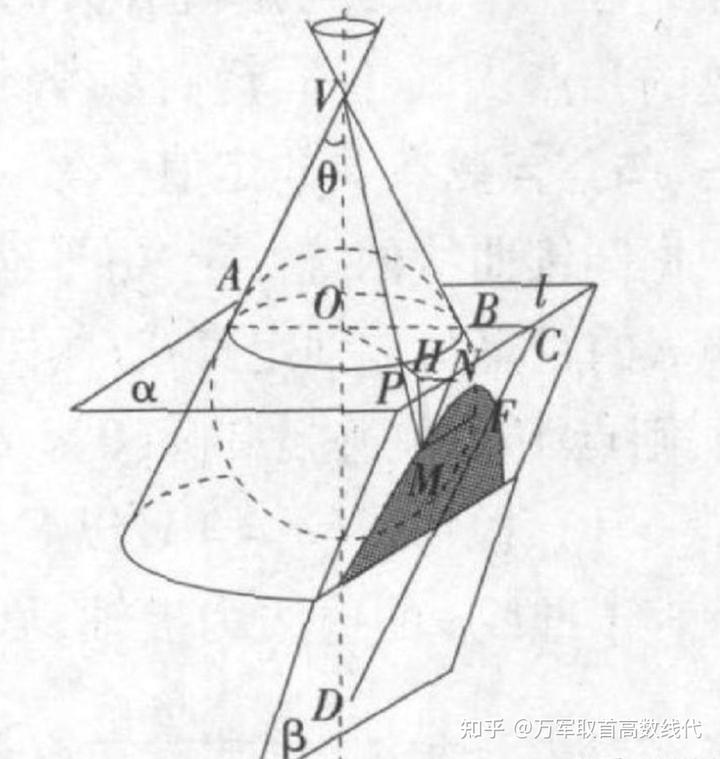
一方面,由于
和
是球的两条切线,我们有
;
另一方面,做
平面
,
,则由于
, 有平面
。
因此,
是
在平面
内的射影,
是
与平面
所成的角,由于
(因为都是平面
的垂线),它等于圆锥的半顶角
。
与此同时,
(两直线平行,内错角相等)。因此三角形
和三角形
全等,
。
这样就证明了
,它符合抛物线的定义。
(这种情况应该是最复杂得了,因为涉及很多平行线和垂直线,要用好平面和轴夹角等于圆锥半顶角这个条件,因为上一句话是个等式,所以定量的成分比较多)
最后就是双曲线。
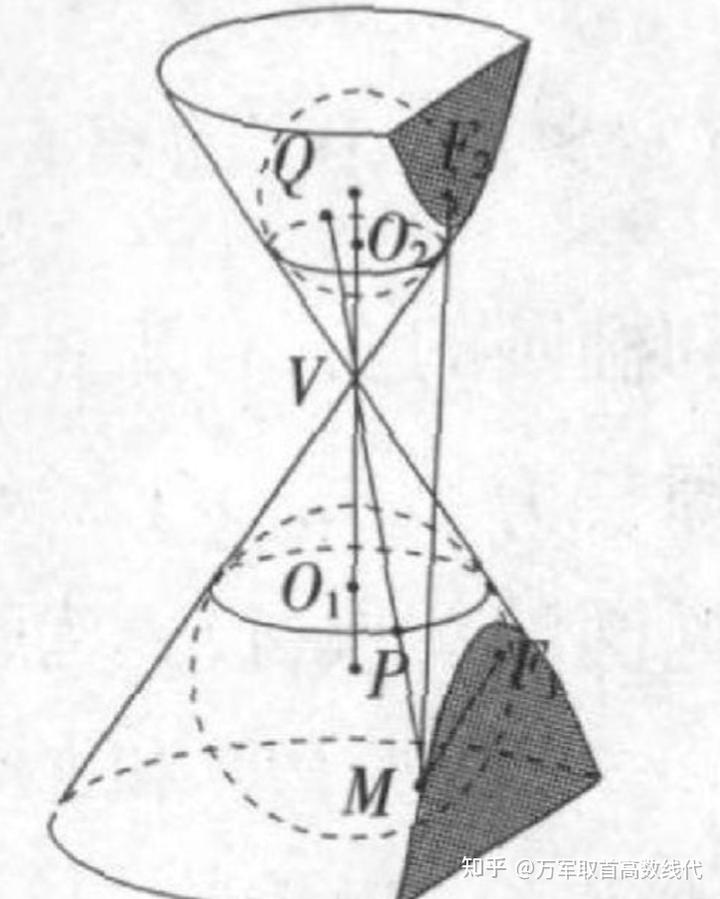
这次比较简单。只需证明
即可。截口曲线
至于截口曲线可能是圆或者两条直线的证明?虽然它们太简单,但是我还是要说:圆对应于截面垂直于轴的情况,而两条直线是圆锥的两条母线。
这里给大家一个思考题:如何证明圆柱的截口曲线是椭圆呢?(答案:两个球都是与圆柱面和截面相切的球,得到的两个切点就是椭圆的两个交点,和圆锥是类似的)
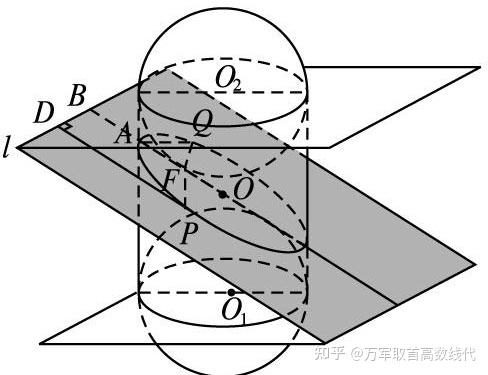
最后,如果你不希望有这么多几何证明,我可以来个代数一点的:
(椭)圆锥面的一般方程,可以从个圆锥面得到。(当然,由于椭圆锥面是圆锥面伸缩得到的,而圆锥曲线伸缩得到的仍然是圆锥曲线,因此,椭圆锥面的截口曲线也是等效的)
一个形式最简单的圆锥面方程,就是
。通过一个可逆线性变换,我们得到
代表的一定是椭圆锥面(如果
线性无关)。由于圆锥面可以任取,即使平面固定为
,它也足以表示任意截口曲线。
代入
后,这就是二次曲线。因此,圆锥曲线(二次曲线)的统一方程,化简后是
。利用这个二次型矩阵的相似对角化,我们可以得到这个曲线的属性。
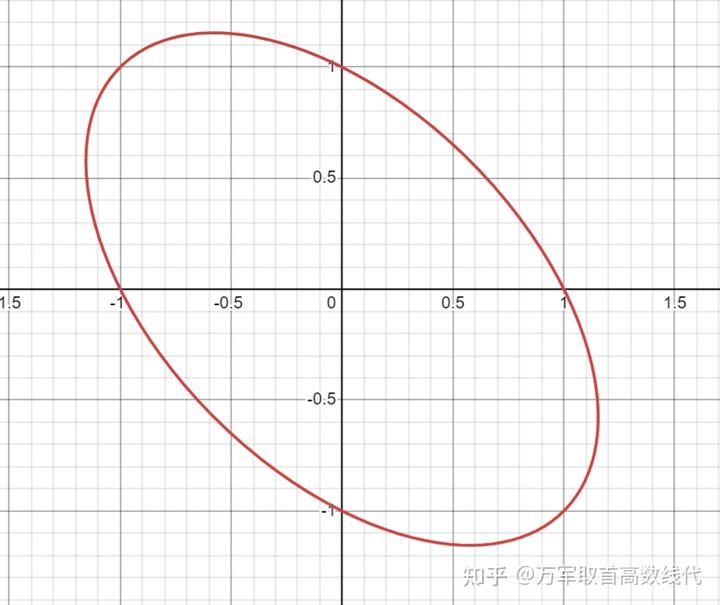
例如,上面的曲线
就是一个椭圆。