椭圆没有周长?

平面椭圆,一个神奇的图形。
小时候的我,觉得椭圆就是一个普普通通的图形。直到我上了高中,接触了圆锥曲线,经历了一番摧残之后,我觉得我似乎认清了椭圆的真面目。而现在,我又碰到了椭圆积分,才发现我真的太天真了......所以,我现在对椭圆充满敬畏之情,不知道何时又会碰到与之有关的更为高深的知识。下面我们就从椭圆的周长开始,慢慢揭开椭圆积分的神秘面纱......
- 问题的引入:椭圆的周长
如果我没记错的话求平面曲线的弧长应该是导数的基本应用之一吧。首先,我们来回忆一下计算平面曲线弧长的公式。
设一连续可微的平面曲线
的参数方程为:
我们取这个曲线
上的一段微元并记作
。有勾股定理可得:
而:
带入
的表达式有:
两边同时积分可得:
这就是有关参数方程的弧长公式了。我们先小试牛刀,计算一下圆的周长。
我们知道,圆的标准参数方程是(其中
为圆的半径):
则:
代入弧长公式有:
一切过程都十分顺利,那我们再来看看椭圆:
椭圆的标准参数方程大家肯定也不会陌生(其中
为半长轴长,
为半短轴长):
我们仅计算椭圆在第一象限的部分的弧长,之后在乘以
就好了。但是第一象限部分的参数的取值范围会有变化,即在第一象限中
。参数方程的导数为:
代入到弧长公式中得到:
直到现在,仍一切顺利,我们在化简一下看看:
......嗯?这玩意怎么处理?到这一步会发现根号完全去不掉,原函数也找不到。到此,本文结束。
嘿嘿,开个玩笑。聪明的数学家们是不可能就此罢休的,于是他们又开始将上面的式子进一步化简:
其中: 叫做椭圆的离心率。
式还可做变量代换:
则:
则有变量代换后的积分:
还可以写的更有强迫症一点:
到现在,椭圆积分的雏形已经出现了。
2. 椭圆积分的诞生
经过 等数学家的研究,椭圆积分的知识体系渐渐完善,直到
的出现彻底彻底完善了椭圆积分的知识体系。
我们先观察 式,这个式子是椭圆周长的积分公式,而它可以被拆成两部分:
我们将拆开后的第一部分拿出来,并去掉积分上下限和系数得到不定积分:
再将第二部分拿出来,去掉系数和积分上下限得到另一个不定积分:
另外还有个一个不定积分:
这三个不定积分便是 所总结得到的。若将上面的三个不定积分做变量代换:
则:
(这个我不知道怎么来的...)
上面的 分别叫做
第一类,第二类,第三类椭圆积分。
之后 又定义了三类
椭圆积分,是将
椭圆积分里面的
换回
得到的,即:
参数 叫做椭圆积分的模。
特别的,当 或
时,这三类椭圆积分都称为完全椭圆积分,否则称为不完全椭圆积分,即:
完全 椭圆积分:
完全 椭圆积分:
3. 椭圆的周长公式
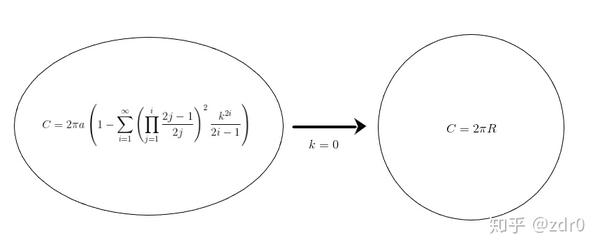
椭圆并非没有周长,只不过没有精确值罢了。对于其周长公式,是一个无穷级数的形式:
其中: 为半长轴长,
为椭圆的离心率。这个级数是由第二类椭圆积分展开所得到的。(可惜我不会展开)。可见,当离心率为零时,级数退化为圆的周长公式。
当然,椭圆的周长公式有几个近似公式:
- 利用算数平均值近似:(精度较低)
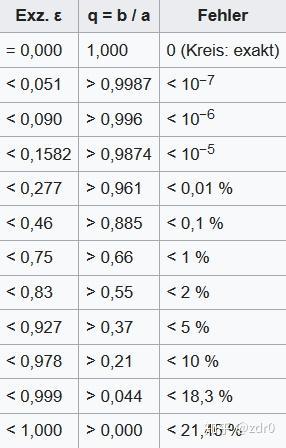
- 利用平方均值近似:(精度一般)
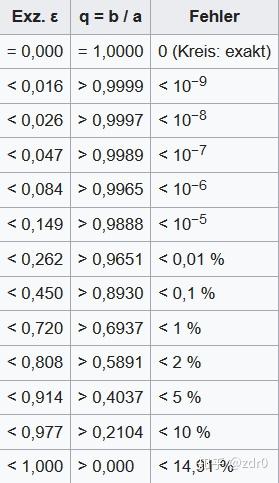
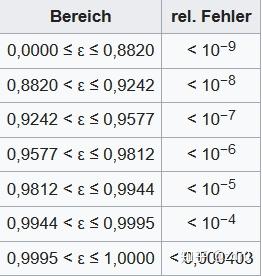
近似公式:(精度很高)
还有没关注专栏《数学及自然科学}》的朋友们请赶快关注吧!您的支持是我最大的动力!