信息物理学中，信息计算能耗的理论下限“兰道尔极限”可以作为这个问题的出发点，即擦除

信息最少需要消耗

能量——无论信息操作的具体过程。

从而我们可以暂时规避对神经元和硅器件的细节讨论，从信息物理学的视角出发来审视人脑和计算机这两种不同体系的差别。这些差别（比如并行计算、稀疏连接等）实际上是使人脑计算中需要更少的信息擦除，从而更节能。

兰道尔原理

兰道尔原理（Landauer's principle）是关于信息计算能耗的理论下限的物理原理。

它认为，任何逻辑上不可逆转的信息操作过程，如擦除一个比特的信息或合并两条计算路径，一定伴随着信息处理设备或其环境的非载信息自由度的相应熵增。^[1]而通常，熵的增加采取的形式就是能量输入到计算机中，被转化为热能，然后散发到环境中。^[2]

我们可以设想这么一个实验（这个实验实际上一种类似西拉德发动机的设备，西拉德发动机是麦克斯韦妖思想实验的一种简化版本）。^[3]

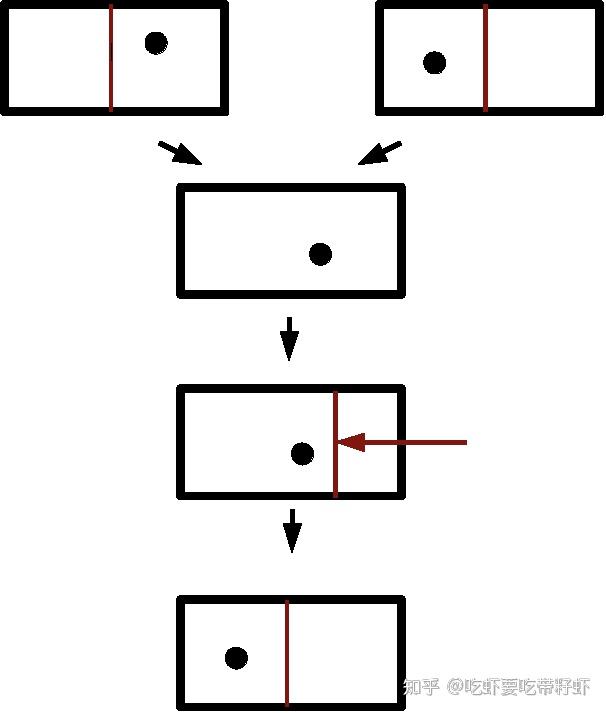
假设我们有一个下图这样的箱子，这个箱子有一个分隔隔板，将箱子分为左侧和右侧。那么我们可以用分子在左侧表示 0，分子在右侧表示 1。所以通过将单个分子放入这个箱子中，我们就存储了一比特（

）的信息。

正如电脑硬盘一样，我们知道真正要擦除存储的信息，事实上你需要用新的信息去覆盖它。

这个实验中也一样，所谓信息的“擦除”意味着，无论这个箱子一开始带有的信息是 0 还是 1（在左或在右），我们现在将要这个箱子设置为 0 来覆盖原有的信息（即擦除）。

也就是说，无论这个分子最初是在左侧还是右侧，我们现在要把这个分子移到左侧。

那么要怎么操作呢？我们可以突然移除分隔隔板，然后慢慢用活塞压缩这个单分子“气体”，直到分子明确位于左侧。这样我们就完成了对原信息的一个“擦除”。

那么根据玻尔兹曼熵公式，

S 是熵，k 是玻尔兹曼常数，W 是微观状态数目。

在我们推动活塞的过程中，分子能占据的空间显然是从箱子的体积

变成了箱子的一半体积

，因此我们也可以认为这个“气体”的微观状态数目从

变成了

.

于是我们能够得到信息擦除过程中，熵的变化为：

也就是说，在我们擦除这个信息的过程中，熵减少了

。如果我们这个操作是在等温环境中进行的，那么这个过程我们需要做的功就是：

这就是兰道尔极限，即擦除

信息最少需要消耗

能量。

这个原理对于人脑和计算机同样适用。所以在擦除 1bit 信息消耗的能量有同样限制的情况下，大脑要更节能，就要在计算过程中涉及更少的“擦除信息”。

正如评论区 @Arete 指出的那样，事实上，上面这个实验设想的是完全理想的条件，在实际体系中，人脑和计算机的能量消耗都还离兰道尔极限较远。不过通过兰道尔的想法，我们可以将信息和能耗直接联系起来，进而从信息的角度出发来考察人脑和硅电子计算机这两种不同的体系的信息处理能耗（而暂时规避对神经元、电子器件具体原子分子机制的讨论）。

人脑和计算机的不同

我们下面就基于信息物理学视角来审视人脑与计算机的区别和能源效率之间的关系：

1. 并行处理：人脑以高度并行和分布式的方式处理信息，许多神经元和突触同时工作。这种并行性允许高效的计算，无需频繁地重置或擦除个别信息位。相比之下，传统计算机主要进行顺序处理，通常需要频繁的内存操作和位擦除。显然这导致了计算机会有更高的能源消耗。

2. 稀疏连接：大脑中的神经元表现出稀疏连接，意味着并非所有神经元都同时活跃或相连。这种稀疏性减少了不断重置或更新信息的需求，因为只有一小部分神经元参与特定任务。相比之下，数字计算机可能需要更频繁地操作和更新内存中的数据，产生额外的能源成本。

3. 自适应可塑性：大脑可以根据学习和经验适应和重构其神经连接。这种适应性使大脑能够针对特定任务优化其电路，而无需频繁擦除内存。传统计算机具有固定的体系结构，通常需要更能源密集的内存更新来适应新任务。

4. 模拟处理：大脑中的神经元以模拟方式（或者有些学者将其看作模拟 + 数字混合的方式）运作，允许连续的近似计算。这降低了对高精度计算的需求。而在数字计算机中，计算都以精确的二进制运算开展，因此它依赖于更精确的、更多的信息擦除操作。相比之下，大脑能耗可能更低。

至于大脑有这一系列特点的原因可能是进化选择，作为一个自组织系统，大脑需要更节能才能更长久地维持神经系统、人体的长期存在。^[4]