大脑皮层舒展开了，你漫步在热带雨林……

停停停，你的大脑皮层它就不能完全展开成平面，因为它的高斯曲率不为 0。

要解释这后面的原理啊，我们可以先看看世界地图：

这是我们的家园，现在为了方便学生学习，我们要做成一个平面的地图：

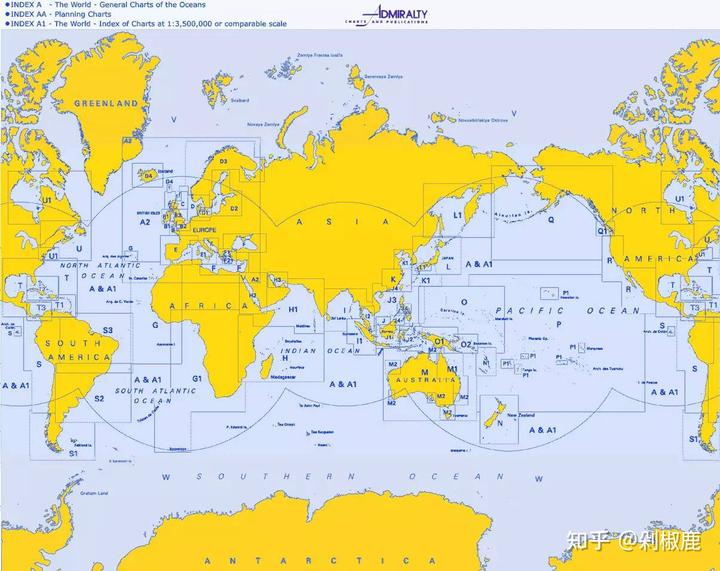
喜欢地理的朋友肯定知道我们要说什么了。

对的，因为球形的地球是没法在不变形的情况下完全展开成平面图形，所以地图都是比例错误的。

以最常用的墨卡托投影（Mercator Projection）举例：

这种投影是正轴等角圆柱投影（形状准确）但面积失真严重，高纬度地区被放大得很夸张，比如格陵兰看起来几乎和非洲一样大。

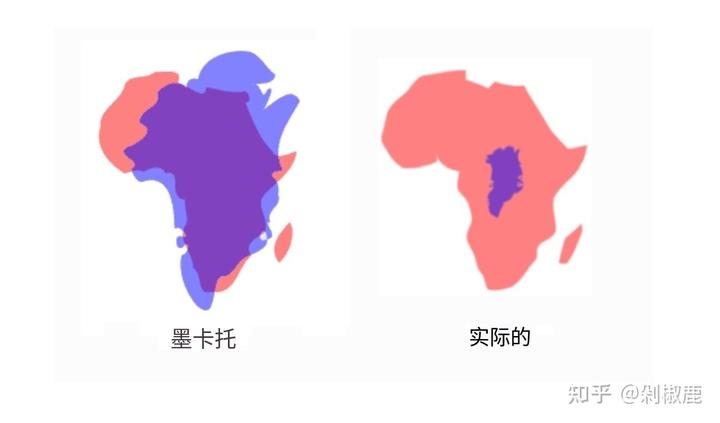
这真是神奇，为什么要这样做呢？

前面说到，球体是不能平展成平面的，要不然你可以试试家里的橘子皮：

你不管把橘子皮掰开成多小的块，它都始终有弧度，你不能得到一块完全平整的橘子皮。

好了，现象有了，现在我们要去寻找原理。

没错，我们的数学王子高斯当年也曾遇到过同样的问题。

高斯绝妙定理（Gauss theorem egregium）

故事要从 19 世纪初说起。

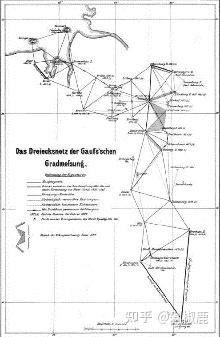
1820 年 5 月 9 日，当时，卡尔·弗里德里希·高斯接受了汉诺威国王的委托，负责一项艰巨的任务：

对汉诺威王国进行大地测量。

这项工作的目标是绘制出精确的王国地图。在那个时代，这意味着要带着经纬仪等测量设备，翻山越岭，在不同的山顶和地标之间建立三角测量网络，精确测量它们之间的距离和角度。

高斯是一个完美主义者。

在测量过程中，他很快就遇到了一个根本性的问题：地球是弯曲的，而地图是平坦的。他记录在地球表面的三角形（由三个山顶等地标构成）的内角和，总是略大于 180 度。这是一个由地球曲率造成的必然结果。

当他试图将这些在曲面上测量得到的数据转换到一张平坦的地图上时，麻烦就来了。他发现，无论用什么方法，都不可能在保持所有距离和角度都完全不变的情况下，将一块弯曲的球面“铺平”。这种转换必然会导致某种形式的变形——要么距离被拉伸或压缩，要么角度发生变化。

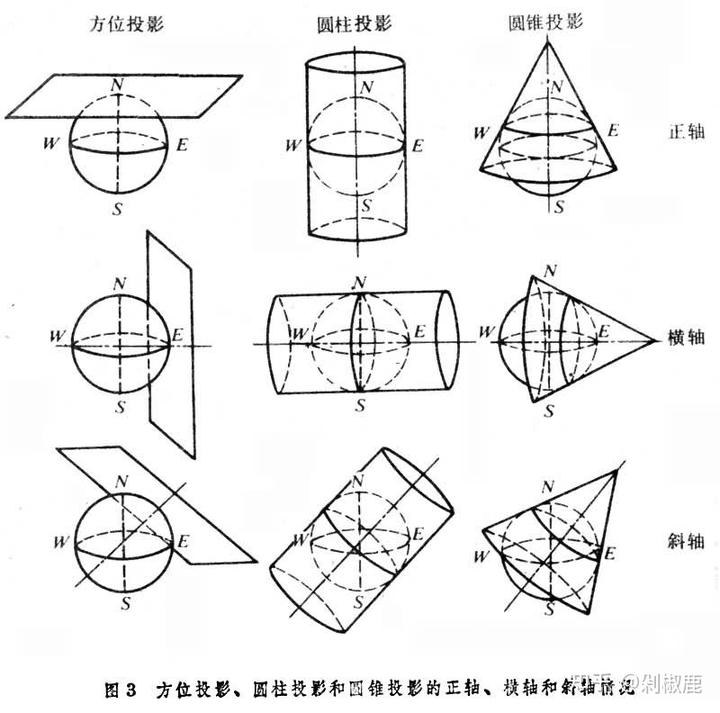
在当时，数学界普遍认为，一个曲面的“弯曲程度”（即曲率）是一个外部属性。

也就是说，要描述一个曲面的弯曲，你必须想象自己是一个身处三维空间中的观察者，从“外部”去看这个曲面是如何在空间中弯折的。例如，一个圆柱和一个平面，从外部看，它们的弯曲形态显然不同。

但高斯开始思考一个更深刻的问题：有没有一种方法，可以仅仅通过在曲面内部进行测量（比如测量距离和角度），就能确定这个曲面的弯曲程度，而完全不需要知道它在外部三维空间中的样子？

换句话说，假设有一只二维的“虫子”生活在一个曲面上，它无法跳出来观察全局。这只虫子仅凭在自己世界里“拉绳子”测量距离，能否判断出自己是生活在一个平面上，还是一个球面上？

为了解决这个问题，高斯发展出了一套强大的数学工具，也就是我们今天所说的微分几何。他定义了两种描述曲面性质的“基本形式”：

第一基本形式：

它描述了曲面内在的度量性质。你可以把它理解为曲面上的“勾股定理”，它告诉你如何在曲面上计算曲线的长度和两条曲线的夹角。这正是那只二维虫子可以测量到的所有信息。

第二基本形式：

它描述了曲面外部的弯曲性质，即曲面是如何嵌入到三维空间中的。

高斯通过复杂的计算，试图找到这两种形式之间的联系。

然后他发现了一个让他自己都震惊的定理：

他发现，一个被他命名为“高斯曲率”（Gaussian Curvature）的量，虽然其最初的定义依赖于第二基本形式（即外部弯曲），但它竟然可以完全只用第一基本形式及其导数来表示！

高斯本人对这个发现的重要性感到非常自豪，他在论文中称之为“Theorema Egregium”，在拉丁语中意为“卓越的定理”或“绝妙的定理”，这个名字也一直沿用至今。

那在生活中的应用就很直观了，我们只需要通过计算就能发现哪些形状是可以延展成平面的，哪些不能。

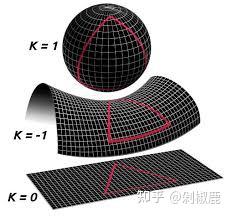
不管是球形还是马鞍型还是薯片型，它们 K 都不等于 0，只有 K=0 的形状才能展开成平面。

比如圆柱形、圆锥形等等。

所以回到问题上，显然咱们大脑的高斯曲率 K 值不等于 0。

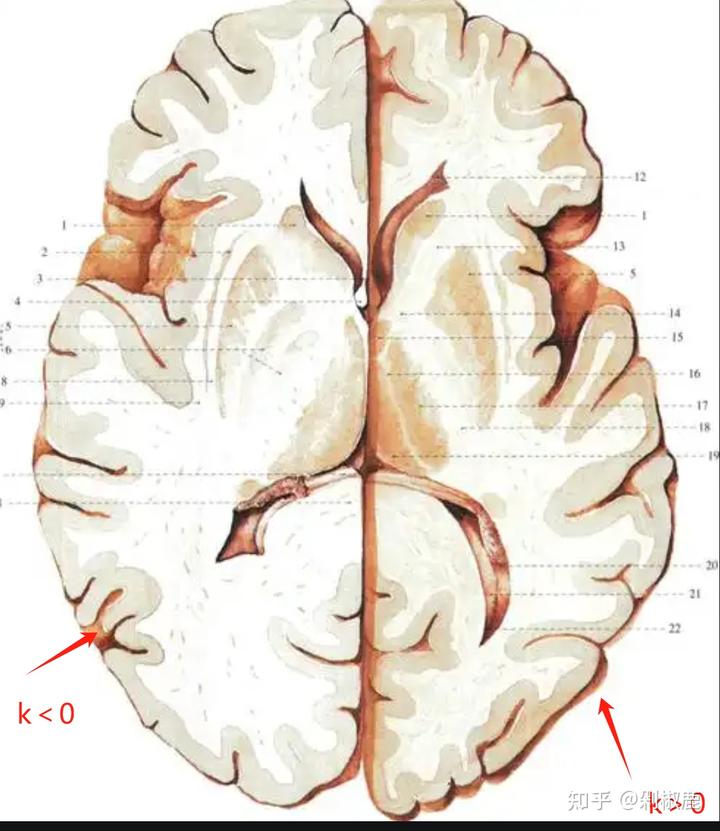
我们可以把大脑皮层的表面想象成一个起伏的“地形”，把它切片成若干小块：

脑回 (Gyrus)：这些是大脑表面凸起的“山峰”或“山脊”。在这些区域的顶点，曲面像球面一样向各个方向都向外凸出。因此，它的高斯曲率 K > 0。

脑沟 (Sulcus)：这些是凹陷下去的“山谷”或“沟壑”。在这些区域，情况更为复杂：

在一些点，比如沟壑的交汇处或弯曲处，曲面会像马鞍一样，在一个方向上向上弯曲，而在另一个方向上向下弯曲。这些“鞍点”的高斯曲率 K < 0。

在一些相对平坦的区域，或者在沟壑深处类似圆柱内壁的地方，其高斯曲率约等于 0。

所以我们的大脑是无法在不产生形变的情况下均匀展开的。

如果强行展开就会出现一个问题：脑花会碎掉一部分。

这些碎掉的部分可不得了了，比如额叶的脑回参与决策和规划，颞叶的脑回与听觉和记忆相关。顶枕沟附近的脑回则负责视觉信息整合。

强行展开意味着这些功能都会破坏掉，即便是展开成了差不多的面积，但是功能已经完全不能用了。

话说有种天生的疾病就叫做无脑回畸形 Lissenceohaly：

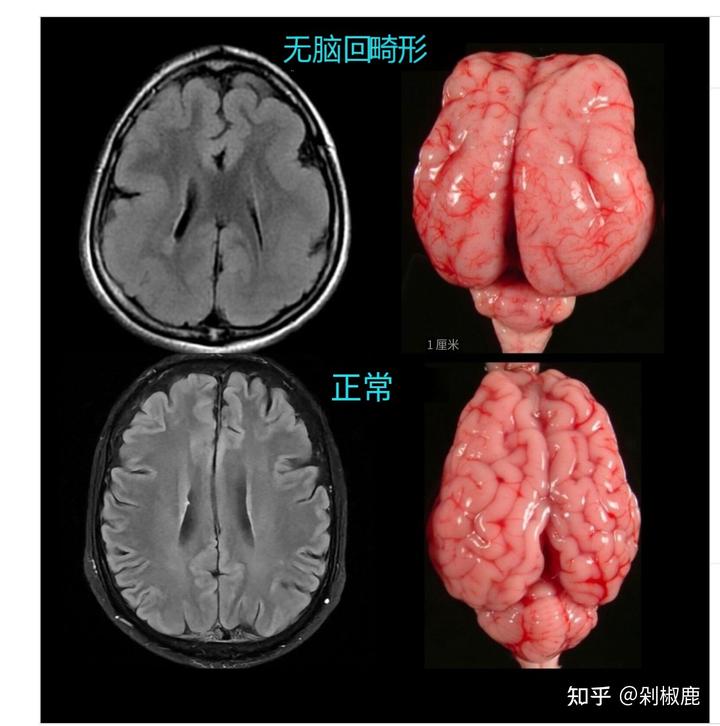
常引起出生后癫痫发作，严重智力障碍，喂养困难，生长迟缓，运动活动受损等。

这种患儿的大脑表面就像是舒展开的，比较光滑，缺乏沟回。

所以大脑皮层舒展开并不是什么好事情……

以上