这个问题挺有趣的。其实，找圆的圆心，最直接的方法就是利用中垂线，随便找到两个圆上的弦，然后找到弦的中点，再在中点画一个垂线，两个垂线交点就是圆心，但是考虑到题目中尺子没有刻度，显然找不到弦的中点，而且没有直角，也画不出垂线，所以这个方法不行。

可以这样， 比如下图中的蓝色区域是问题中的一把尺子，尺子无刻度，无直角。黑色圈是一个标准的圆，先用这个尺子在圆上任找四个交点，我们分别记作 ABCD，并画两条直线 AD 和 BC，如下图。

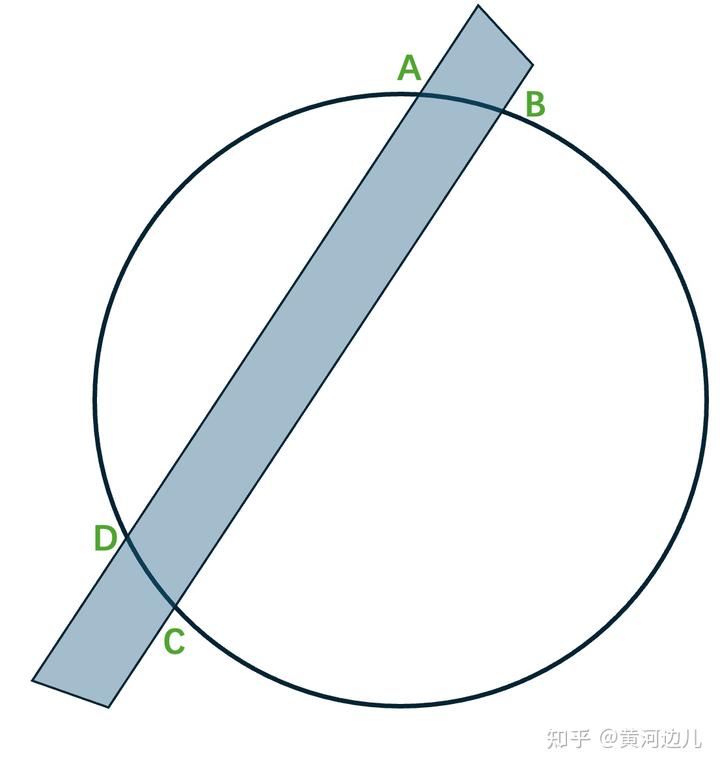
第二步，然后在用这把尺子，过 A 点和 C 点，在画两条直线 AA‘和 CC'，如下图，两次左图在圆内产生两个交点，O 和 O‘，然后沿着 OO’做线，如红线，这条线必过圆心。

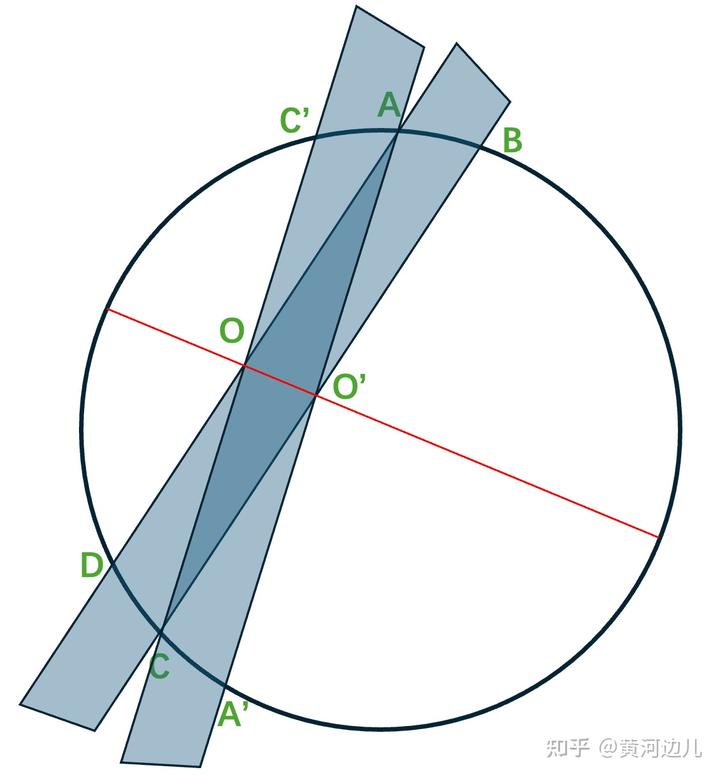
第三步，沿着红线和圆的交点 E 和 F，E 点在上，F 点在在下，再用该尺子做两条线 EE'和 FF'，如下图，

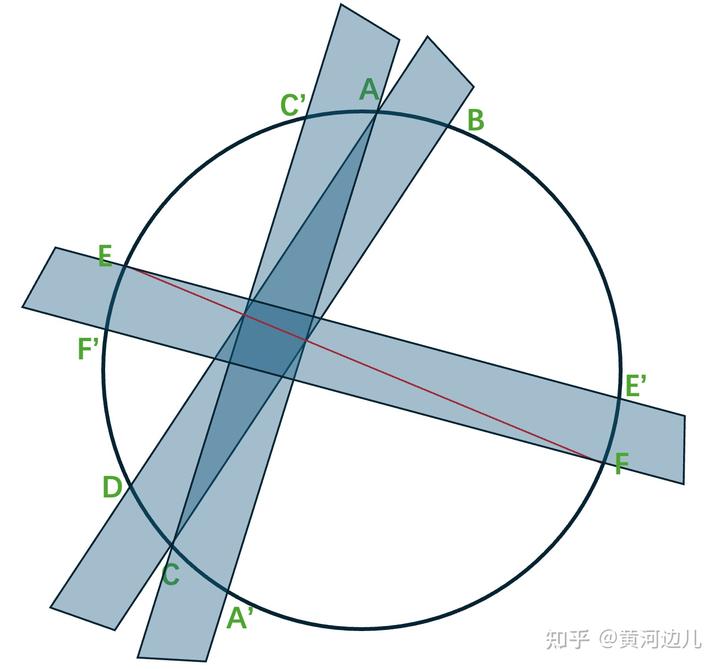
然后，继续沿着 E 和 F，E 点在下，F 点在上，再用该尺子做两条线如下图，这样我们就得到一个菱形。

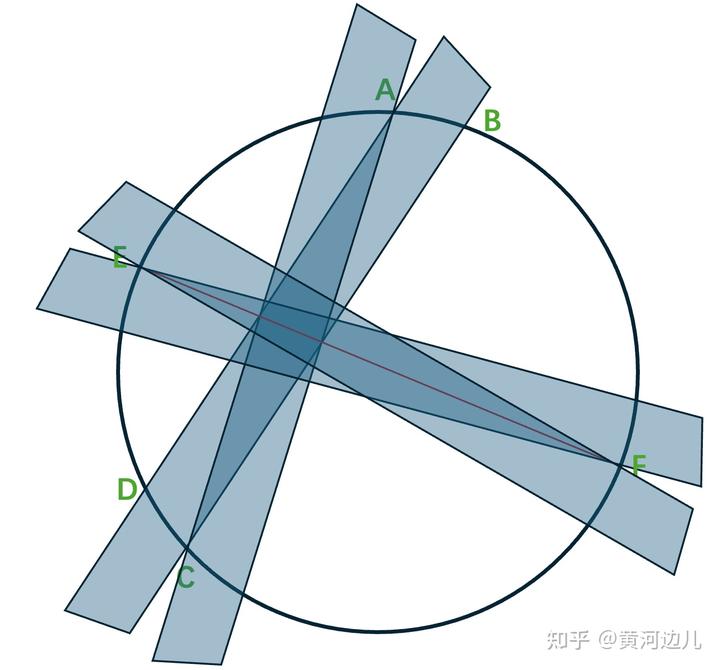
最后，这个菱形的中心就是该圆的圆心，如下图，黑色箭头所指的红线交点处，就是圆心。

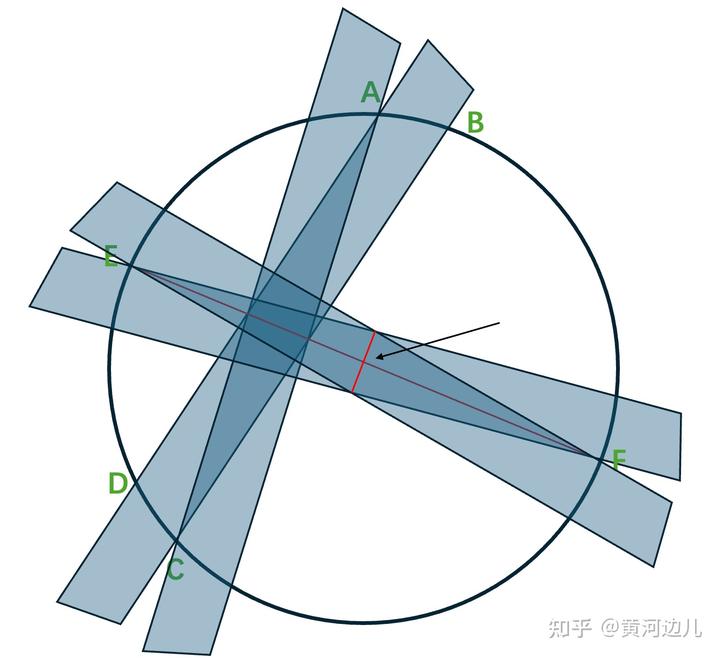
当然，如果圆在纸上，可能一种直观的方法就是把纸对折，对折两次，保证半圆重合，这样形成两条直径，两线交点就是圆心，这样甚至不需要直尺也能找到圆心，但是不是所有的圆都是在纸上找圆心的，所以回到题目本身，上述方法是一个通用的可行方法，可以只用一个没有刻度的尺子找到圆心。

好了，写到这里~

感谢评论区， @爱吃西瓜不吐皮 问到了“为什么第二步红线必定过圆心”。是这样，先做两条辅助线，Aa 和 Cc，如下图所示。 Aa 垂直于 CC‘， Cc 垂直于 AD，因为都是一个尺画出来的两条线，所以 Aa=Cc，进而很容易得到直角三角形 AaO 全等于直角三角形 CcO，于是也就有了 CO 等于 AO。

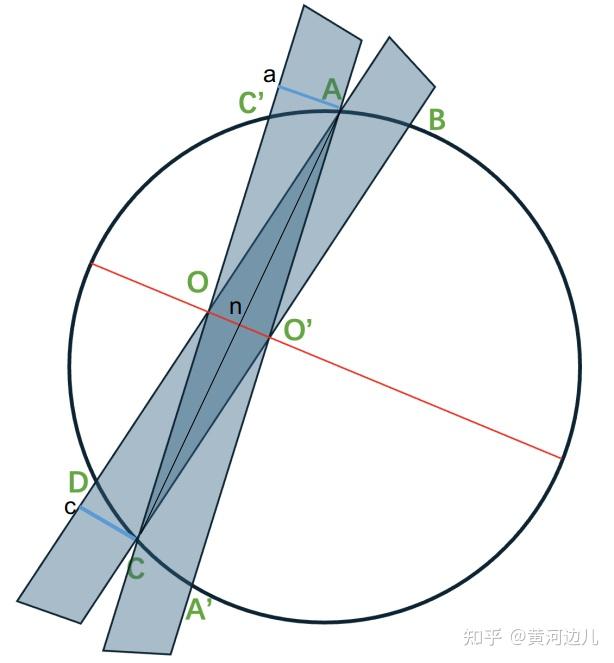
所以，我们就得到了平行四边形 AOCO‘是一个菱形，想要证明红线过圆心，只需要证明红线垂直且平分了弦 AC，显然作为菱形的对角线，An 等以 Cn，且 OO‘垂直于 AC，所以，红线 OO‘一定过圆心。其实，第五步里提到的第二条红线过圆心也是同样的道理。