如何用最少的圆周率 π、自然常数 e 凑出 2025?

看我用计算机终结这个问题。

用 e 和π构造 2025 需要的数字、一元运算最少使用个数为 6,一共有24 种互不等价的组合方式。并且可以证明,如果不考虑 Beta 函数和积分符号,不存在使用个数为 5 的可能。
注:不考虑 Beta 函数是因为这是二元运算,但是要被计入使用个数。我懒得单独写 case,就把这个情况忽略了。积分则是太麻烦了,不好处理。
更新说明
原始回答发布于 UTC+8:2024 年 3 月 16 日 01 时。
- 原始回答只列出了 22 种互不等价的凑法,对应了式 1 到式 21。
更新版 V1 回答发布于 UTC+8:2024 年 3 月 16 日 15 时。
- 感谢 @Richard Xu 在评论区的指正,经过检查代码发现代码误将边界条件 -1e14 写成了 1e-14,从而漏掉了
这组解作为式 22。经过核验校对,两版代码只在此处有差异,其他解都保持不变。
- 感谢 @深巷明朝卖杏花 在评论区的指正,本回答在将计算机输出转为 TeX 代码,误将式 3 的括号抄错了位置。
- 本版代码经过校对,修正了一些文法错误和公式抄录错误,并发现了第一版抄录时遗漏了式 23,现已经补上。
更新版 V2 回答发布于 UTC+8:2024 年 3 月 16 日 15 时。
- 新增了不含取整函数的凑法
不含取整函数的凑法
看到评论区有说不含取整函数优雅后,我打算不用计算机,手凑一个不含取整函数的表达式。当然,既然没有取整函数,我们的整数就只能通过 来凑了,相当于用两次机会可以表示出一个数字 1。
基于 @Nabiuta 的回答中因式分解的思路,可以做一个简单的优化。注意到 ,有
。一共用了 12 个 1,所以记为 24 次。
能不能再给力点?当然可以。注意到 ,所以
。一共用了 10 个 1 和 1 个双阶乘,所以记为 21 次。
还能再给力点吗?当然可以,大家坐稳咯。现在我们要来一个 trick 了。众所周知 ,
。因此有
,注意到
,有
。一共用了 7 个 1、1 个双阶乘、1 个π、1 个 arccsc,所以记为 17 次。
等等,真的需要 2=1+1 这么凑吗?我看未必。注意到 ,我们有了究极形态的凑法!
,仅需 13 次操作就能无取整得到 2025!甚至和题目例子的次数一样!
好了,我没活了,13 次已经是我的极限了。剩下的交给大佬们操作吧,让我们把目光转回有取整函数的组合。
完整结果展示
在这些组合中,我觉得最优美的一种凑法是 ,只用到了
,并且全是一元运算符,十分优雅。
只含 的凑法为:
。
只含 的凑法为:
。
所有有效凑法如下:
为什么说一共有 24 种互不等价的组合方式,但这里只写了 23 个公式呢?因为我只认为能用算术运算交换律、结合律和分配律合并规约的运算是等价的,而第 2 个公式用到的 这个 trick 不算等价,算两种不等价的组合方式。
当然,授人以鱼不如授人以渔。这么多凑法,肯定不是我肉眼观察出来的。我先试了下,一顿乱按计算器,只肉眼观察出来了一组 的解:

上面的 24 种组合是通过计算机穷举得到的,用 C++ 一共穷举了 12 亿多种可能的凑法得到的解,运行了半个小时左右。因为是穷举,这也严格地证明了不存在 的解。当然,我的C++ 代码会放到文末开源给大家,这个代码具有可复用性,其他常数和函数的组合也可以通过此代码求得。
4or5 个数字 or 一元函数能凑出哪些数字
此处仅展示 2000 到 2050 之间的结果,为了节省时间,我就把程序原始输出放出来,不做处理与说明(之前整理结果浪费了我一个小时,太费时间了)。
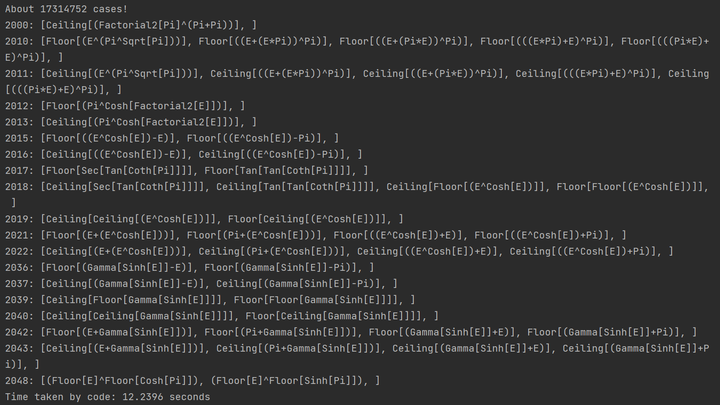
5 个数字 or 一元函数的结果如下:
2000: [Ceiling[(Factorial2[Pi]^(Pi+Pi))], ]
2010: [Floor[(E^(Pi^Sqrt[Pi]))], Floor[((E+(E*Pi))^Pi)], Floor[((E+(Pi*E))^Pi)], Floor[(((E*Pi)+E)^Pi)], Floor[(((Pi*E)+E)^Pi)], ]
2011: [Ceiling[(E^(Pi^Sqrt[Pi]))], Ceiling[((E+(E*Pi))^Pi)], Ceiling[((E+(Pi*E))^Pi)], Ceiling[(((E*Pi)+E)^Pi)], Ceiling[(((Pi*E)+E)^Pi)], ]
2012: [Floor[(Pi^Cosh[Factorial2[E]])], ]
2013: [Ceiling[(Pi^Cosh[Factorial2[E]])], ]
2015: [Floor[((E^Cosh[E])-E)], Floor[((E^Cosh[E])-Pi)], ]
2016: [Ceiling[((E^Cosh[E])-E)], Ceiling[((E^Cosh[E])-Pi)], ]
2017: [Floor[Sec[Tan[Coth[Pi]]]], Floor[Tan[Tan[Coth[Pi]]]], ]
2018: [Ceiling[Sec[Tan[Coth[Pi]]]], Ceiling[Tan[Tan[Coth[Pi]]]], Ceiling[Floor[(E^Cosh[E])]], Floor[Floor[(E^Cosh[E])]], ]
2019: [Ceiling[Ceiling[(E^Cosh[E])]], Floor[Ceiling[(E^Cosh[E])]], ]
2021: [Floor[(E+(E^Cosh[E]))], Floor[(Pi+(E^Cosh[E]))], Floor[((E^Cosh[E])+E)], Floor[((E^Cosh[E])+Pi)], ]
2022: [Ceiling[(E+(E^Cosh[E]))], Ceiling[(Pi+(E^Cosh[E]))], Ceiling[((E^Cosh[E])+E)], Ceiling[((E^Cosh[E])+Pi)], ]
2036: [Floor[(Gamma[Sinh[E]]-E)], Floor[(Gamma[Sinh[E]]-Pi)], ]
2037: [Ceiling[(Gamma[Sinh[E]]-E)], Ceiling[(Gamma[Sinh[E]]-Pi)], ]
2039: [Ceiling[Floor[Gamma[Sinh[E]]]], Floor[Floor[Gamma[Sinh[E]]]], ]
2040: [Ceiling[Ceiling[Gamma[Sinh[E]]]], Floor[Ceiling[Gamma[Sinh[E]]]], ]
2042: [Floor[(E+Gamma[Sinh[E]])], Floor[(Pi+Gamma[Sinh[E]])], Floor[(Gamma[Sinh[E]]+E)], Floor[(Gamma[Sinh[E]]+Pi)], ]
2043: [Ceiling[(E+Gamma[Sinh[E]])], Ceiling[(Pi+Gamma[Sinh[E]])], Ceiling[(Gamma[Sinh[E]]+E)], Ceiling[(Gamma[Sinh[E]]+Pi)], ]
2048: [(Floor[E]^Floor[Cosh[Pi]]), (Floor[E]^Floor[Sinh[Pi]]), ]
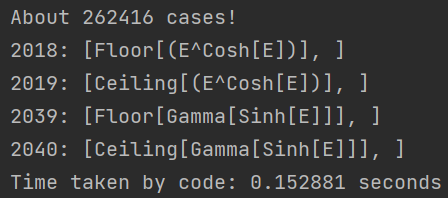
4 个数字 or 一元函数的结果如下:
2018: [Floor[(E^Cosh[E])], ]
2019: [Ceiling[(E^Cosh[E])], ]
2039: [Floor[Gamma[Sinh[E]]], ]
2040: [Ceiling[Gamma[Sinh[E]]], ]
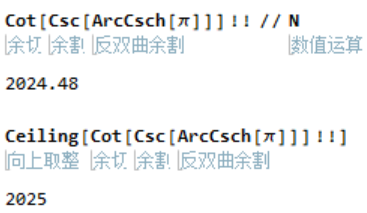
还有一个有趣的现象,虽说 ,但实际上
,非常接近 2024。
穷举所用的 C++ 代码
这个代码应该挺好懂的,用法很简单。通过 register_num 函数、 register_op2 函数和 register_op1 函数分别注册常数、二元运算和一元运算,通过 rpn_pattern_op 函数生成所有符合要求的逆波兰表达式模式串,最后通过 rpn_one_pattern 基于每个模式串生成真正的逆波兰表达式,最后就是求解和呈现的部分了。
要求: C++ 版本大于等于 C++17 ,因为用到了结构化绑定的语法特性,也可以通过等价的语法去掉,最低 C++ 版本可以降到 C++11 ,但是我懒得降。
注:本穷举代码没有考虑运算表达式的对称性约化、等价化简和剪枝,因为我懒,语法树这个东西谁爱写谁写吧。
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
map<string, double> num_map; // 数字
map<string, function<double(double)> > op1_map; // 一元运算
map<string, function<double(double, double)> > op2_map; // 二元运算
void register_num(string str, double num) {
num_map[str] = num;
}
void register_op1(string str, function<double(double)> op1) {
op1_map[str] = op1;
}
void register_op2(string str, function<double(double, double)> op2) {
op2_map[str] = op2;
}
// 剩余 p 个数字,q 个符号,0 代表数字,2 代表二元运算
void rpn_pattern_op2_impl(vector<string> &all_pattern, string pattern, int p, int q) {
if (p == 0 && q == 0)
all_pattern.emplace_back(move(pattern));
else if (p >= q)
rpn_pattern_op2_impl(all_pattern, pattern + "0", p - 1, q);
else if (p == 0)
rpn_pattern_op2_impl(all_pattern, pattern + "2", p, q - 1);
else {
rpn_pattern_op2_impl(all_pattern, pattern + "0", p - 1, q);
rpn_pattern_op2_impl(all_pattern, pattern + "2", p, q - 1);
}
}
// m 个数字,m-1 个二元运算,共 Catalan(m-1)种可能
vector<string> rpn_pattern_op2(int m) {
vector<string> all_pattern;
string pattern = ""s;
rpn_pattern_op2_impl(all_pattern, pattern, m, m - 1);
return all_pattern;
}
// 从{0, 1, ..., n-1}中选 k 个数的全组合
vector<vector<int> > combine(int n, int k) {
vector<vector<int>> result;
for (int mask = 0; mask < (1 << n); ++mask) {
if (__builtin_popcount(mask) == k) {
vector<int> current;
for (int i = 0; i < n; ++ i) {
if (mask & (1 << i)) {
current.push_back(i);
}
}
result.push_back(current);
}
}
return result;
}
// m 个数字,m-1 个二元运算,插入 n-m 个一元运算
// 考虑到第一个数字前不能插入一元运算,剩下有 n+m-2 个符号,相当于在 n+m-2 个符号中选出 n-m 个变成一元运算,剩下的保持原先顺序
// 一共(n+m-2)!/[m!*(m-1)!*(n-m)!],其中 m 从 1 到 n 求和
// {1, 2, 6, 22, 90, 394, 1806, 8558}
vector<string> rpn_pattern_op(int n) {
vector<string> all_pattern_op;
for (int m = 1; m <= n; ++ m) {
vector<string> all_pattern_op2 = rpn_pattern_op2(m);
vector<vector<int> > combines = combine(n + m - 2, 2 * m - 2);
for (const auto &pattern_op2: all_pattern_op2) {
for (const auto &now_combine: combines) {
string pattern_op(n + m - 1, '1');
pattern_op[0] = '0';
for (int i = 0; i < 2 * m - 2; ++ i) {
pattern_op[now_combine[i] + 1] = pattern_op2[i + 1];
}
all_pattern_op.emplace_back(move(pattern_op));
}
}
}
return all_pattern_op;
}
// 估计有多少个 rpn 表达式会被生成
long long rpn_estimate(int n) {
// 生成全部模式串,0 代表数字,1 代表一元运算,2 代表二元运算
vector<string> all_pattern = rpn_pattern_op(n);
// 代入具体值,转换成逆波兰表达式
long long ans = 0;
for (const auto &pattern: all_pattern) {
long long num = 0;
long long op1 = 0;
long long op2 = 0;
for (auto chr: pattern) {
switch (chr) {
case '0': ++ num; break;
case '1': ++ op1; break;
case '2': ++ op2; break;
}
}
ans += round(pow(num_map.size(), num) * pow(op1_map.size(), op1)) * pow(op2_map.size(), op2);
}
return ans;
}
// {0,1,...,m-1}^n
vector<vector<int>> gen_cart_product(int m, int n) {
vector<vector<int> > result;
vector<int> current(n, 0);
while (true) {
result.push_back(current);
int idx = n - 1;
while (idx >= 0 && ++current[idx] == m) {
current[idx] = 0;
--idx;
}
if (idx < 0)
break;
}
return result;
}
// 生成有 n 个数字或一元运算符的全部表达式
map<double, vector<string> > rpn_one_pattern(string pattern_op) {
map<double, vector<string> > ans;
int num = 0;
int op1 = 0;
int op2 = 0;
for (auto chr: pattern_op) {
switch (chr) {
case '0': ++ num; break;
case '1': ++ op1; break;
case '2': ++ op2; break;
}
}
auto num_list = vector<pair<string, double> >(num_map.begin(), num_map.end());
auto op1_list = vector<pair<string, function<double(double)> > >(op1_map.begin(), op1_map.end());
auto op2_list = vector<pair<string, function<double(double, double)> > >(op2_map.begin(), op2_map.end());
// 说明只有二元运算符
vector<vector<int> > all_num_comb, all_op1_comb, all_op2_comb;
all_num_comb = gen_cart_product(num_map.size(), num);
if (op1 == 0)
all_op1_comb.emplace_back(vector<int> {0});
else
all_op1_comb = gen_cart_product(op1_map.size(), op1);
if (op2 == 0)
all_op2_comb.emplace_back(vector<int> {0});
else
all_op2_comb = gen_cart_product(op2_map.size(), op2);
for (const auto &num_comb: all_num_comb) {
for (const auto &op1_comb: all_op1_comb) {
for (const auto &op2_comb: all_op2_comb) {
int i_num = 0;
int i_op1 = 0;
int i_op2 = 0;
stack<double> nums;
stack<string> fmt;
for (auto chr: pattern_op) {
switch (chr) {
case '0': {
nums.push(num_list[num_comb[i_num]].second);
fmt.push(num_list[num_comb[i_num]].first);
++ i_num;
break;
}
case '1': {
double val = nums.top(); nums.pop();
function<double(double)> func = op1_list[op1_comb[i_op1]].second;
string val_str = fmt.top(); fmt.pop();
fmt.push(op1_list[op1_comb[i_op1]].first + "[" + val_str + "]");
++ i_op1;
double new_val = func(val);
if (!isfinite(new_val) || new_val > 1e14 || new_val < -1e14)
goto next_loop;
nums.push(new_val);
break;
}
case '2': {
double rhs = nums.top(); nums.pop();
string rhs_str = fmt.top(); fmt.pop();
double lhs = nums.top(); nums.pop();
string lhs_str = fmt.top(); fmt.pop();
function<double(double, double )> func = op2_list[op2_comb[i_op2]].second;
fmt.push("("s + lhs_str + op2_list[op2_comb[i_op2]].first + rhs_str + ")"s);
++ i_op2;
double new_val = func(lhs, rhs);
if (!isfinite(new_val) || new_val > 1e14 || new_val < -1e14)
goto next_loop;
nums.push(new_val);
break;
}
}
}
ans[nums.top()].emplace_back(move(fmt.top()));
next_loop:;
}
}
}
return ans;
}
int main() {
register_num("E"s, 2.7182818284590452354);
register_num("Pi"s, 3.14159265358979323846);
register_op2("+"s, [](double a, double b){return a + b;});
register_op2("-"s, [](double a, double b){return a - b;});
register_op2("*"s, [](double a, double b){return a * b;});
register_op2("/"s, [](double a, double b){return a / b;});
register_op2("^"s, [](double a, double b){return pow(a, b);});
register_op1("Sqrt"s, [](double x){return sqrt(x);});
register_op1("Sin"s, [](double x){return sin(x);});
register_op1("Arcsin"s, [](double x){return asin(x);});
register_op1("Cos"s, [](double x){return cos(x);});
register_op1("Arccos"s, [](double x){return acos(x);});
register_op1("Tan"s, [](double x){return tan(x);});
register_op1("Arctan"s, [](double x){return atan(x);});
register_op1("Cot"s, [](double x){return 1/tan(x);});
register_op1("ArcCot"s, [](double x){return atan(1/x);});
register_op1("Sec"s, [](double x){return 1/cos(x);});
register_op1("ArcSec"s, [](double x){return acos(1/x);});
register_op1("Csc"s, [](double x){return 1/sin(x);});
register_op1("ArcCsc"s, [](double x){return asin(1/x);});
register_op1("Sinh"s, [](double x){return sinh(x);});
register_op1("ArcSinh"s, [](double x){return asinh(x);});
register_op1("Cosh"s, [](double x){return cosh(x);});
register_op1("ArcCosh"s, [](double x){return acosh(x);});
register_op1("Tanh"s, [](double x){return tanh(x);});
register_op1("ArcTanh"s, [](double x){return atanh(x);});
register_op1("Coth"s, [](double x){return 1/tanh(x);});
register_op1("ArcCoth"s, [](double x){return atanh(1/x);});
register_op1("Sech"s, [](double x){return 1/cosh(x);});
register_op1("ArcSech"s, [](double x){return acosh(1/x);});
register_op1("Csch"s, [](double x){return 1/sinh(x);});
register_op1("ArcCsch"s, [](double x){return asinh(1/x);});
register_op1("Log"s, [](double x){return log(x);});
register_op1("Log10"s, [](double x){return log10(x);});
register_op1("Ceiling"s, [](double x){return ceil(x);});
register_op1("Floor"s, [](double x){return floor(x);});
register_op1("Gamma"s, [](double x){return tgamma(x);});
register_op1("Factorial"s, [](double x){return tgamma(x + 1);});
// x!! = 2^{x/2} * (pi/2)^{(cos(pi * x) - 1) / 4} * Gamma(x/2 + 1)
register_op1("Factorial2"s, [](double x){
return pow(2, x/2) * pow(M_PI_2, (cos(M_PI * x) - 1) / 4) * tgamma(x/2 + 1);
});
cout << "About " << rpn_estimate(6) << " cases!" << endl;
auto start = chrono::high_resolution_clock::now();
map<double, vector<string> > ans;
auto all_pattern_op = rpn_pattern_op(6);
for (auto pattern: all_pattern_op) {
auto rpn_res = rpn_one_pattern(pattern);
for (auto &[num, fmt_vec]: rpn_res) {
if (num == 2025) {
for (const auto &fmt: fmt_vec) {
ans[num].emplace_back(fmt);
}
}
}
}
auto end = chrono::high_resolution_clock::now();
for (auto [num, fmt_vec]: ans) {
cout << num << ": [";
for (const auto &fmt: fmt_vec)
cout << fmt << ", ";
cout << "]" << endl;
}
auto duration = chrono::duration_cast<chrono::microseconds>(end - start);
cout << "Time taken by code: " << duration.count() / 1e6 << " seconds" << endl;
return 0;
}