如果把傅里叶变换突然一键删除,世界上会发生什么变化?

你删不掉,除非你能从底层开始重塑整个世界。
你以为的删除傅里叶变换:
假设存在一个「数学橡皮擦」,能够让傅里叶变换彻底消失:
所有教科书、论文、乃至人类大脑中的相关知识都被清空,所有基于它的工程技术也随之崩溃,电子信号处理、通信系统、医学成像、图像的 JPEG 和 MP3 编码统统不复存在,人类社会如大厦之将倾,危如累卵。
但实际上大自然并不在乎你会不会傅里叶变换,它早已深深刻入了现实世界的物理法则之中:
即使所有人类都忘记了傅里叶变换,自然界仍会悄无声息地进行傅里叶变换:夫琅禾费衍射是对光波前的傅里叶变换,甚至我们人类自身对声音的感知、视觉信息的处理也是执行了生物版的傅里叶变换。
傅里叶变换不仅仅是一个数学工具,更是自然界的内禀属性之一,我们只是用数学形式描述了这种普遍存在的现象。因此你不可能真正删除傅里叶变换,除非你能从底层开始重塑整个物理世界的基本规律。
一、光的衍射与傅里叶变换
可能你打死都不会想到,拿着激光照一照,大自然就已经进行了傅里叶变换。
假设你拿起一个带有细缝的物体,拿着一束激光照射,你会发现,在远处的屏幕上,光没有简单地透过物体后形成一个缝的投影,而是出现了一系列明暗相间的条纹。这种现象就被称为光的衍射。
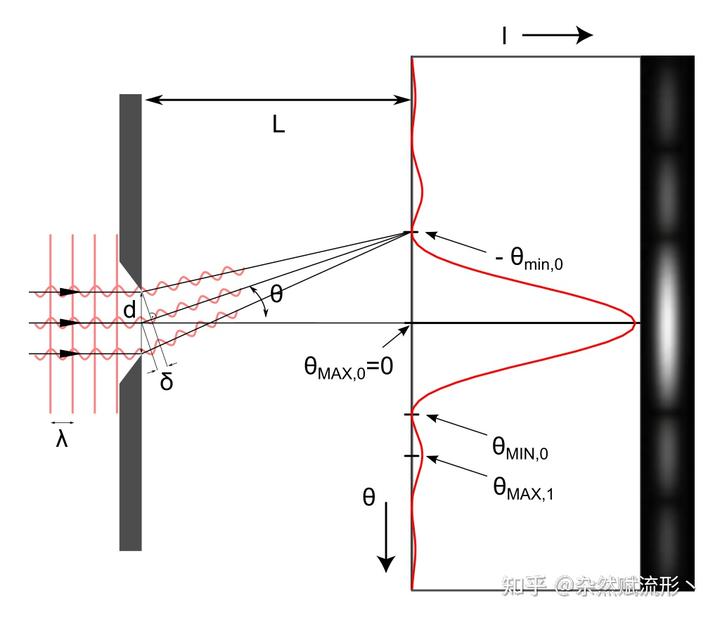
注意:右侧的单缝衍射图样实际上是一个 sinc 函数,它正是左侧单缝(方波函数)的傅里叶变换结果。
现在我们考虑更复杂的情况,不局限于一个简单的狭缝,我们考虑更一般的孔径(它的形状可以千奇百怪)。假设一列(振幅为
)的平面波正入射到下图所示的孔径上,根据惠更斯 - 菲涅耳原理,就可以计算出在距离孔径
处的屏幕
上某点
的场分布。
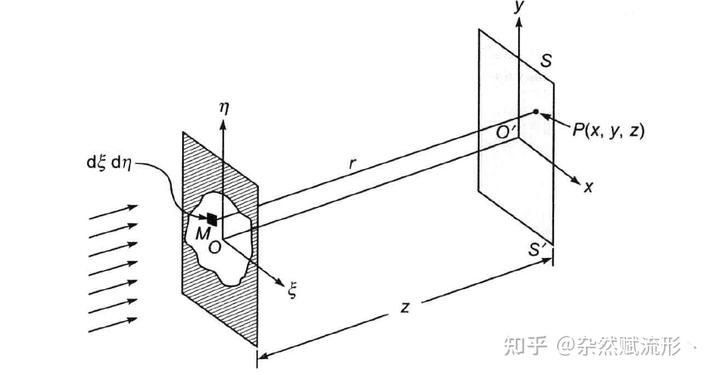
省略掉一系列枯燥的计算和分析[1],我们直接给出接收屏上的场分布
,即菲涅耳衍射积分:
可能读者到目前为止还不知道我们要干什么,我们考虑进一步作简化:如果接收屏与孔径相隔足够远,即
足够大,使得上述积分里的
可以用 1 来替代,我们就可以得到夫琅禾费衍射积分:
细心的你一定发现了,上述等式的右边正是对函数
的二维傅里叶变换,这就告诉了我们一个极其重要的结论:
夫琅禾费衍射图样是对孔径函数
的傅里叶变换![2]
换句话说,当你看见这些衍射条纹时,你其实是在「看到」一个傅里叶变换的结果。
那么我们如何在物理上,通过实验来观察夫琅禾费衍射呢?
回忆初中物理学知识:放置在凸透镜焦平面的光源,经过凸透镜折射后会得到平行光。
那么我们只需要借助两个凸透镜就能在物理上成功实现夫琅禾费衍射。这两个凸透镜的作用是将光源和观察屏移到无限远处,第一个透镜使得光束变为平行光,第二个透镜使得接收到的平行光聚焦于观察屏,如下右图所示。
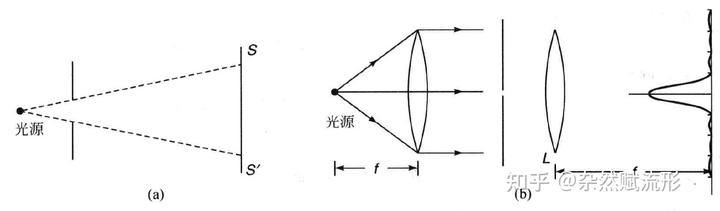
原则上,我们可以通过夫琅禾费衍射积分来解析或者数值地计算出衍射图样。
但作为一个科普性的回答,我们不对具体过程作过多阐述,直接来看实验结果。


觉得陌生吗?
并不是!
这些衍射图样在太空望远镜拍摄的星空图片里经常能看见,也就是我们通常所说的衍射尖峰:

下面两张就是韦伯望远镜拍摄的照片,我们可以从里面发现大量的衍射尖峰(注意有八个角,其中六个比较明显,另外两个较难观察到),这些正是远处的星体发出的光,到达望远镜时发生衍射而造成的。


而哈勃望远镜拍摄的照片只有四个衍射尖峰。

另一方面,我们还可以通过计算机程序模拟,直接对孔径函数
做二维傅里叶变换,来与上述实验结果进行比较。
 不同孔径对应的夫琅禾费衍图样 https://www.zhihu.com/video/1888420939403878546
不同孔径对应的夫琅禾费衍图样 https://www.zhihu.com/video/1888420939403878546
另外,我自己也写了个 Python 程序(代码见文末)。
注意以下绘图结果中为了凸显,已经把左图中的孔径的大小放大了 10 倍,实际孔径要小得多。

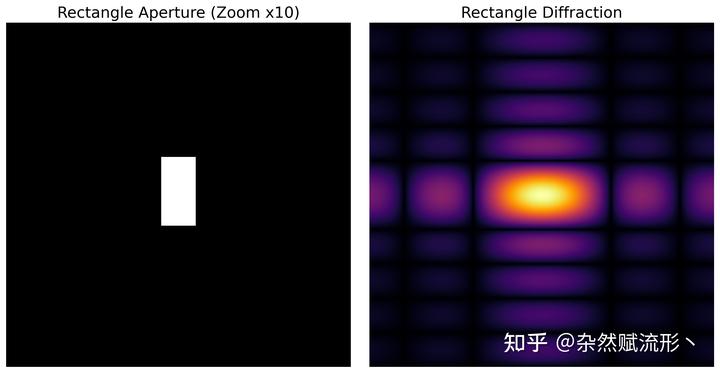
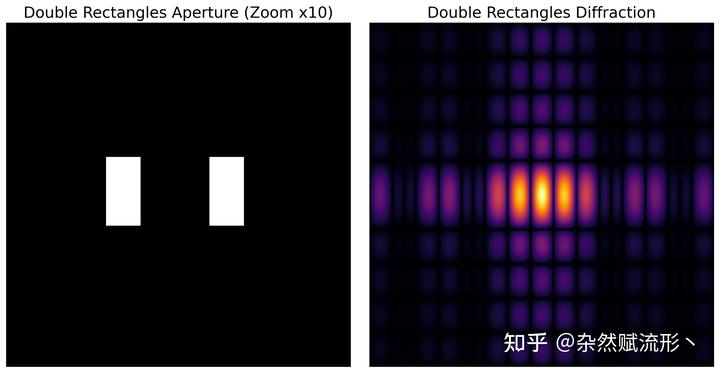

可以看到我们的数值模拟和实验得到的夫琅禾费衍射图样完全吻合。
二、透镜的傅里叶变换性质
除此之外,就连我们最熟悉的透镜也可以从傅里叶光学的角度来解释。
如下图所示,当光场通过透镜
后,透镜的作用是将输入光场
的空间频率分量进行调制,后焦平面
处的光场分布
实际上就是物体(或前焦平面
)光场
的傅里叶变换。
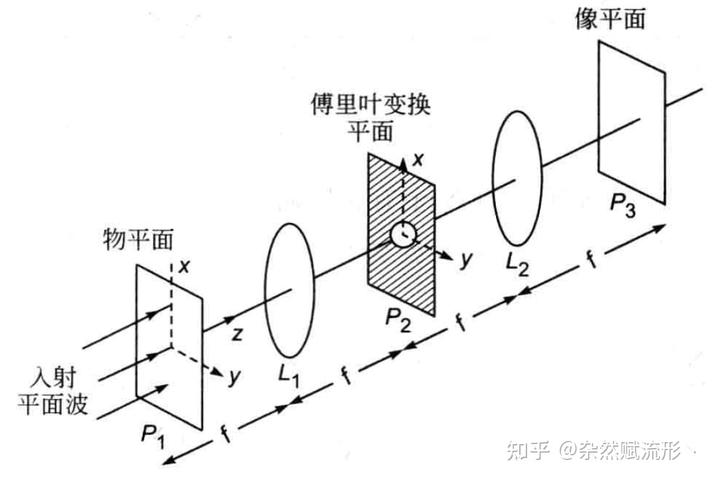
具体而言,
处的场分布和
处的场分布满足关系:
其中
表示空间频率,显然它也是我们前述提到的傅里叶变换形式。我们可以得知另一个重要结论:
校正相差透镜的后焦平面上的场分布是前焦平面上场分布的傅里叶变换![2]
校正像差透镜的这个重要性质构成了空间滤波这门学科的基础,如果我们在后焦平面
处放置一个光屏,仅在光轴附近挖掉一个小孔允许透射的光经过,而其余的光无法透过,如上图所示。那我们就自然而然地过滤掉了高频成分,因为高频成分的光经过透镜折射后是远离光轴的,即
较大。
如果你对初中物理仍留有印象,我们还可以举一个更具体的例子做说明[3]。
假设我们有一束平行光,当它正入射到凸透镜时,它会折射到焦点
上,如下图所示。
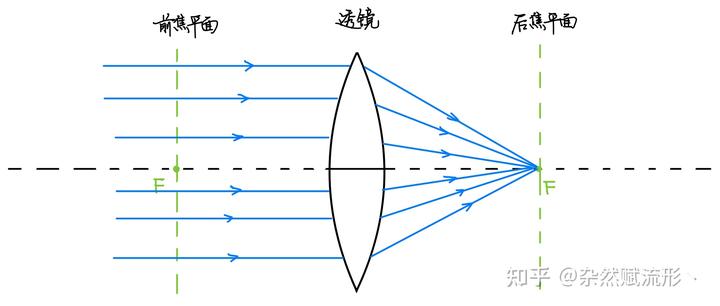
如果我们改变平行光的入射角度,它仍然会汇聚到焦平面上,只是此时不再汇聚到焦点
上,而是偏离了光轴,如下图所示。
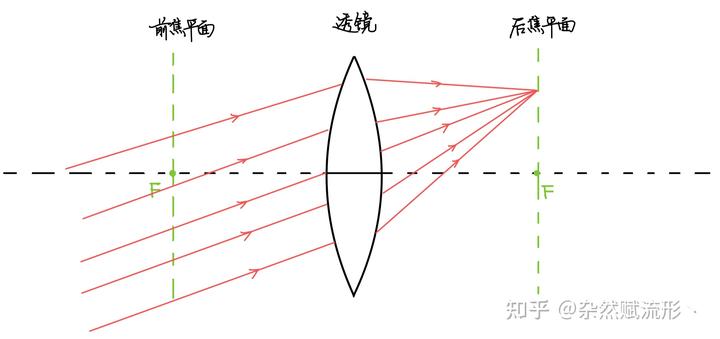
当平行光以不同角度入射时,它的波前可以视为不同相位的平面波。例如一束以光轴成角度
的平面波,其场分布可以表示为:
其中
,此时波前的相位因子对应于空间频率
,满足:
所以不同的入射角度
就对应了不同的空间频率
。而
正是经透镜折射后在后焦平面
上汇聚点的坐标。这就告诉我们,后焦平面上的点位置就直接反映了入射光的空间频率。
例如垂直入射的光
,就对应着后焦平面
的焦点
。
我们可以考虑更复杂的情况,如果有一系列多个角度入射的单色平面波组成的复合光线,我们只要放置一个凸透镜,就可以直接筛选出不同频率的成分!
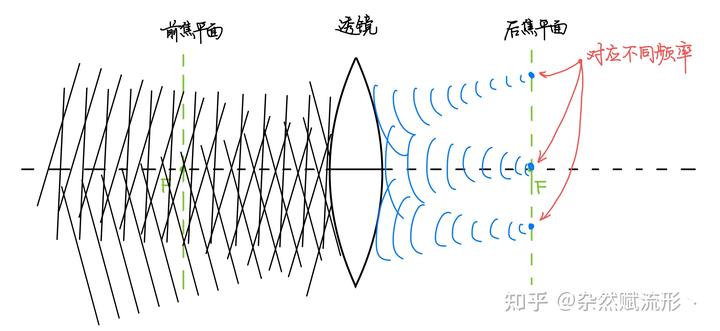
三、结语
第一节和第二节的内容实际上都是傅里叶光学领域的基础知识,感兴趣的同学可以阅读这一领域的相关教科书。
下次当你需要进行傅里叶变换操作时,不妨造出来一个光学系统,大自然会帮你搞定一切!
可能你觉得我在开玩笑。
但请别不相信,在早期计算机并不发达的时候,进行傅里叶变换需要大量的计算资源,人们就是用光学方法来实现傅里叶变换的。光学傅里叶变换的一个重要优势是能够在空间域上并行处理信息,且无需依赖传统的电子计算机的运算能力,从而在当时的技术条件下能高效地完成复杂的运算。虽然它只是一种模拟运算,精度不高,但对于许多应用,其运算精度已经合乎需要。
除此之外,人们也很早就认识到可通过对物体的夫琅禾费衍射图样的测量来确定物体的形状尺寸,尤其对于尺寸较小的物体,直接测量常有困难,尤其需要高精密的光学系统把它放大后测量。然而物体越小(或结构越精细),其频谱越展宽,衍射图样的几何尺寸越大,测量频谱就越容易。发展到今天,光学频谱分析系统已经是实用性很强的系统了[4]。
所以,傅里叶变换你删不掉,大自然已经帮你铭刻好了。
即便人类都已忘却傅里叶变换,通过观察这些光学现象,人们也能逐渐重新揭示其数学结构,甚至或许还能另辟蹊径,创造新的方式来表达「傅里叶变换」。
附录A. 数学,发现还是发明?
既然大自然自身就会进行傅里叶变换的操作,那这就自然而然地引发了一个更深层次的思考:数学是人类发明的,还是宇宙本身的语言?
我此前还特地提了一个问题,欢迎大家讨论。
B. Python 代码
回答中所用来绘制夫琅禾费衍射图样的 Python 代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft2, fftshift
def create_circular_aperture(diameter, size, step=1):
"""创建圆形孔径
step: 网格步长(1=原始分辨率,<1=更高分辨率)
"""
radius = diameter / 2
if step == 1:
y, x = np.ogrid[-size//2:size//2, -size//2:size//2]
distance = np.sqrt(x**2 + y**2)
# mask = distance <= radius
mask = 1 / (1 + np.exp((distance - radius) / 0.8))
# mask = np.zeros_like(distance)
# inner_radius = radius - 0.6
# outer_radius = radius + 0.6
# transition = (distance - inner_radius) / (outer_radius - inner_radius)
# mask[distance <= inner_radius] = 1.0
# mask[(distance > inner_radius) & (distance <= outer_radius)] = 1 - transition[(distance > inner_radius) & (distance <= outer_radius)]
else:
lin = np.linspace(-size//2, size//2, int(size/step))
y, x = np.meshgrid(lin, lin, indexing='ij')
distance = np.sqrt(x**2 + y**2)
mask = distance <= radius
return mask.astype(float)
def create_rectangular_aperture(width, height, size):
"""创建矩形孔径"""
aperture = np.zeros((size, size))
start_x = size//2 - width//2
start_y = size//2 - height//2
aperture[start_y:start_y+height, start_x:start_x+width] = 1
return aperture
def create_double_rectangular_aperture(width, height, size, gap=5):
"""创建水平并列双矩形孔径"""
aperture = np.zeros((size, size))
center_x = size // 2
center_y = size // 2
start_x_left = center_x - (width + gap//2)
start_y_left = center_y - height//2
end_x_left = start_x_left + width
end_y_left = start_y_left + height
start_x_right = center_x + gap//2
start_y_right = center_y - height//2
end_x_right = start_x_right + width
end_y_right = start_y_right + height
aperture[start_y_left:end_y_left, start_x_left:end_x_left] = 1
aperture[start_y_right:end_y_right, start_x_right:end_x_right] = 1
return aperture
def create_triangular_aperture(side_length, size, step=1):
"""创建等边三角形孔径
step: 网格步长(1=原始分辨率,<1=更高分辨率)
"""
angle = np.pi/3
if step == 1:
y, x = np.ogrid[-size//2:size//2, -size//2:size//2]
else:
lin = np.linspace(-size//2, size//2, int(size/step))
y, x = np.meshgrid(lin, lin, indexing='ij')
aperture = ((-y + side_length/(2*np.cos(angle/2))-np.tan(angle)*(x) > (0))
& (-y + side_length/(2*np.cos(angle/2))+np.tan(angle)*(x) > (0))
& (-y + side_length/(2*np.cos(angle/2)) < (side_length*np.cos(angle/2))))
return aperture
def calculate_diffraction(aperture, Gamma=0.4):
"""计算衍射图样"""
field = fftshift(fft2(aperture))
intensity = np.abs(field)**2
intensity = intensity / np.max(intensity) # 归一化
intensity = intensity**Gamma
return intensity
def plot_aperture_and_diffraction(aperture, title, Gamma=0.4, display_aperture=None, zoom_factor=10):
"""绘制孔径和衍射图样
aperture: 用于计算衍射的孔径
display_aperture: 用于显示的孔径(可选),如果不提供则使用 aperture
Gamma: 用于增强衍射图样较弱的部分
"""
diffraction = calculate_diffraction(aperture, Gamma)
display = display_aperture if display_aperture is not None else aperture
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 左侧孔径放大
axes[0].imshow(display, cmap='gray')
axes[0].set_title(f'{title} Aperture (Zoom x{zoom_factor})',size=18)
axes[0].axis('off')
size = display.shape[0]
axes[0].set_xlim(size//2 - size//(2*zoom_factor), size//2 + size//(2*zoom_factor))
axes[0].set_ylim(size//2 + size//(2*zoom_factor), size//2 - size//(2*zoom_factor))
# 右侧衍射图样
axes[1].imshow(diffraction, cmap='inferno')
axes[1].set_title(f'{title} Diffraction', size=18)
axes[1].axis('off')
plt.tight_layout()
plt.savefig(f"Fig/{title}.png", bbox_inches='tight', dpi=300)
plt.show()
# 参数设置
size = 512
# 创建并绘制不同孔径
circular = create_circular_aperture(12, size)
display = create_circular_aperture(12, size, 0.1)
plot_aperture_and_diffraction(circular, 'Circle', Gamma=0.23,display_aperture=display)
rectangular = create_rectangular_aperture(5, 10, size)
plot_aperture_and_diffraction(rectangular, 'Rectangle',Gamma=0.36)
double_rectangular = create_double_rectangular_aperture(5, 10, size,gap=10)
plot_aperture_and_diffraction(double_rectangular, 'Double Rectangles',Gamma=0.36)
triangular = create_triangular_aperture(10, size, 0.45)
display = create_triangular_aperture(10, size, 0.1)
plot_aperture_and_diffraction(triangular, 'Triangle', Gamma=0.36, display_aperture=display)