抽象代数可以用来解决很多游戏问题，特别是单人解谜游戏。很多单人解谜游戏可以抽象为棋盘状态的置换（Permutation），这些置换通常可以组成一个群或者有限域。

以下介绍一个可以使用抽象代数来解决的解谜游戏。

独立钻石棋（Peg Solitaire)

该游戏又名“孔明棋”。游戏道具是这样一个棋盘：

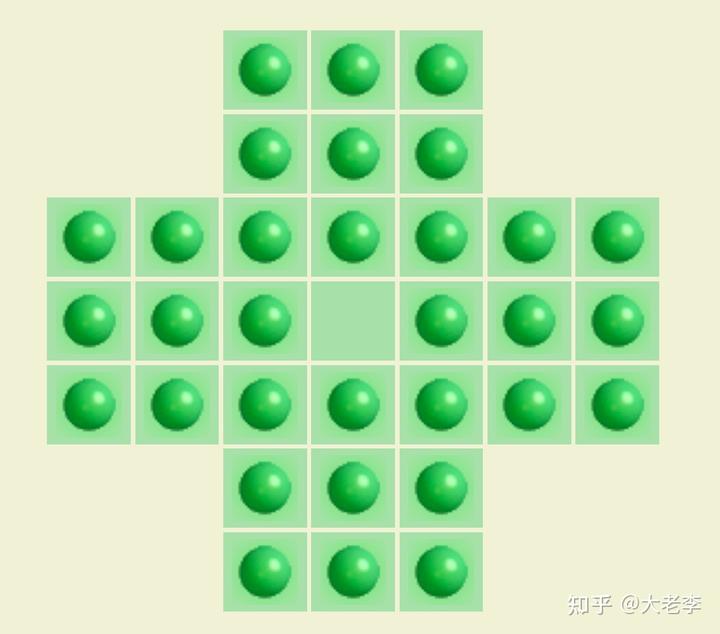
规则是，每次移动一个棋子，跳过另一个棋子并落入空格中，移除被跳过的棋子。以下是一组从开始状态之后，可能的移动过程：

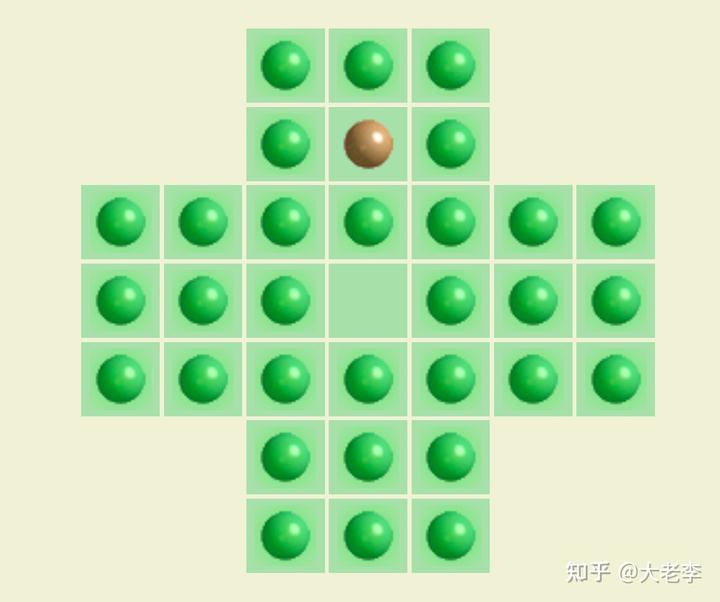
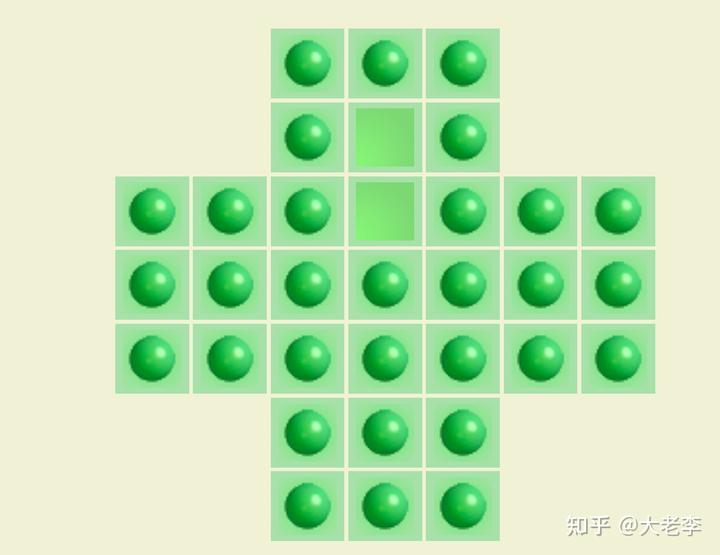
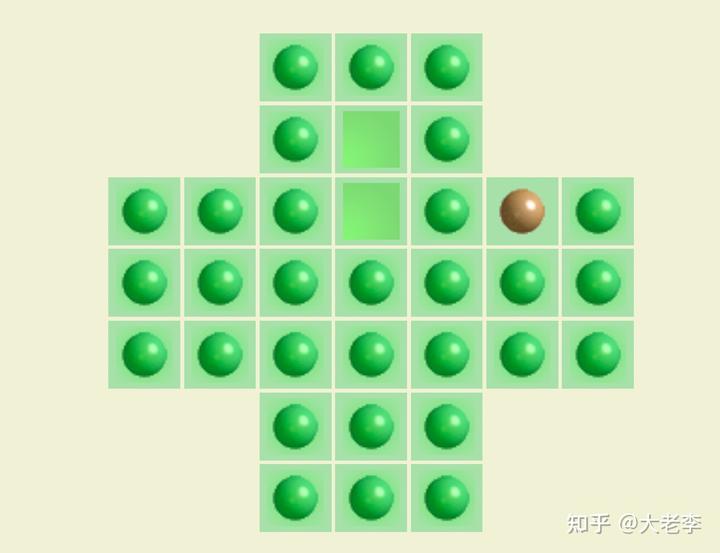
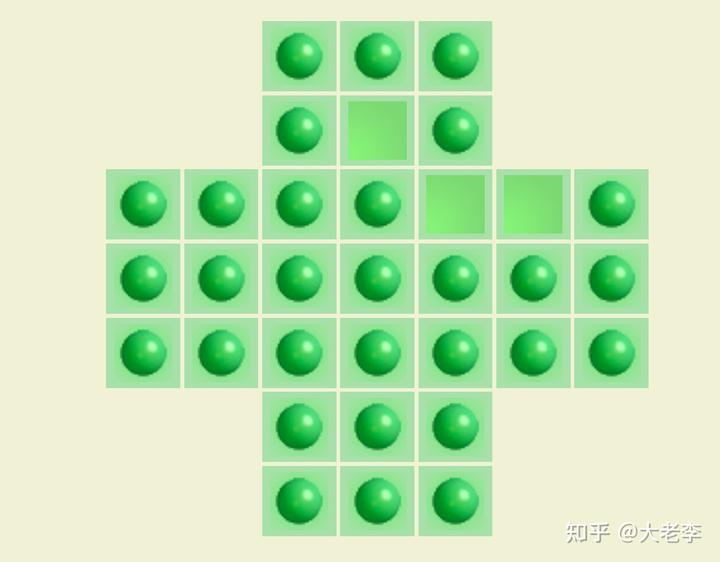
游戏目标是使得最终棋盘上只剩一个棋子，且这个棋子恰好位于棋盘中央为最佳。据说最短的玩法是 18 步（连续移动同一个棋子算 1 步）。

本文不考虑最短的玩法，只论证这个结论：

独立钻石棋中，如果最终只剩 1 个棋子，则该棋子只可能位于如下 5 个红色五角星位置之一：

此结论用有限域（Finite Field）理论证明相当简单。唯一需要的准备知识是克莱因四元域 。

克莱因四元域是四个元素构成的集合，其中有加法和乘法两种运算，运算规则如下：

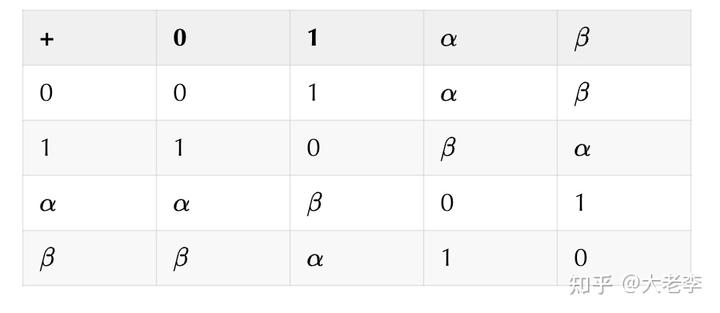
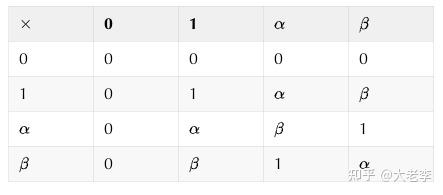
此处无需关心

和

的具体含义，仅仅是两个符号。可以验证，在以上运算规则下，我们熟悉的加法和乘法的交换律，结合律和分配律等都成立。

现在来证明之前关于独立钻石棋的结论。首先将棋盘上的位置标上坐标：

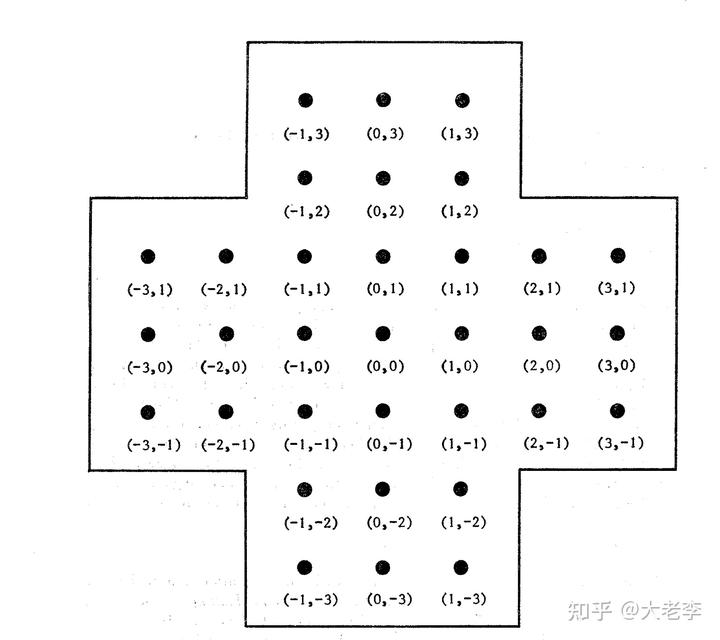
定义这样两个函数，定义域是棋盘上一组棋子位置 X，每个棋子的坐标用(x,y)表示；值域是克莱因四元域：

此时的妙处在于，如果按钻石棋的规则移动棋子，使棋局从 X 局面变化为 Y 局面时，以下等式总是成立（请自行验证）：

，

而游戏初始局面时，

。所以当终局时，如果只剩一个棋子，其坐标值(x,y)必须满足：

根据之前的运算表，

，所以

和

必须是 3 的倍数，因此最终棋子坐标值只能是以下 5 种之一：

结论得证！（严格来说，以上只是证明了这些位置的必要性，充分性还未证明，不过通过实践，可以证明这些位置都是可达的。）

希望这篇文章能让你感受到一些抽象代数的魅力。

参考链接：https://alexandria.tue.nl/repository/freearticles/598441.pdf

2025.3.14 更新：

看到有人问具体解法的，随便（让 AI）写了个程序，找了一个解法，做成了 manim 动画，给大家看看：

https://www.zhihu.com/video/1884180859336242410

由于这个游戏的每一步的合法选择与当前状态有关，所以我没有想到什么好的，可以用数学快速求解的方法。