人耳可以听到的频率上限约为 20 kHz（请留意单位的大小写一定不能错）。根据奈奎斯特采样定理 (Nyquist Sampling Theorem) ，将一个连续的信号（模拟信号）离散化，高于采样频率的一半的部分会发生混叠 (Aliasing)，造成信号的失真。所以人耳听到的 20 kHz 需要至少 40 kHz 的采样频率。

可是这是个理论上的数值。在现实生活中并不存在完美的狄拉克 delta 函数，同时，我们进行数模转换的时候是采用的是算力需求最小的零阶保持 (zero order hold) 的策略（也就是维持当前值，直到接收到下一个参数）。

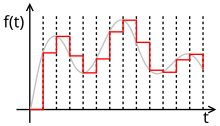
但是这样的波形文件如果你仔细放大看，他就成方形的了。

这边我们需要用到一个理想的低通滤波器，也就是一个矩形脉冲函数 (Boxcar function) 。

他经过傅里叶变换以后变成辛格函数 (Sinc function)，而 sinc 函数在重建时有个缺点，那就是在奈奎斯特频率的部分会有个大约 4 dB 的衰减( sinc(1/2) = sin(π/2)/(π/2)=1/(π/2) = 2/π ，20log(2/π) = -3.92 dB) 。

请留意在信号领域 sinc x = sin (πx)/(πx)，而不是数学课上学的 sinc x = sin (x)/x

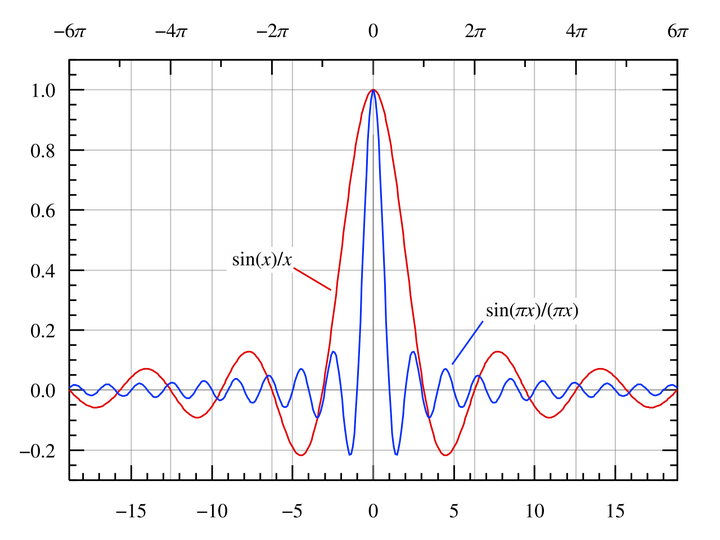
这显然不是我们想要的。因为我们希望的是他在整个奈奎斯特频段都不要出现衰减才对。

可是，这里面有个很严重的问题，也感谢评论区今日绫波明日香同学的提醒。

因为现实中是做不出理想低通滤波器的。

如果我们摆烂干脆不用低通滤波器，初始的输入信号高频部分高于原先的奈奎斯特频率的部分会被错误的“折叠”到低频区域。

当时行业惯使用的是一个简单但是好用的解决方案，那就是巴特沃斯滤波器 （Butterworth Filter）。当然这个解决方案现在早已淘汰了。

这是他的电路图：

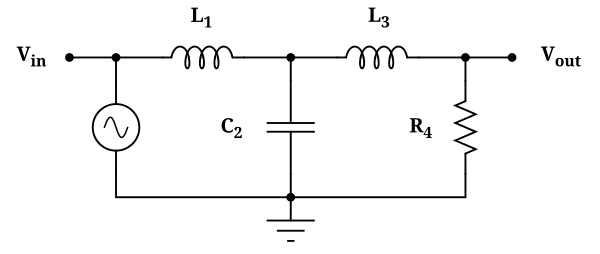
这个设计太绝妙了，只需要电阻，电容，电感就可以了。

这是他的波特图 (Bode Plot):

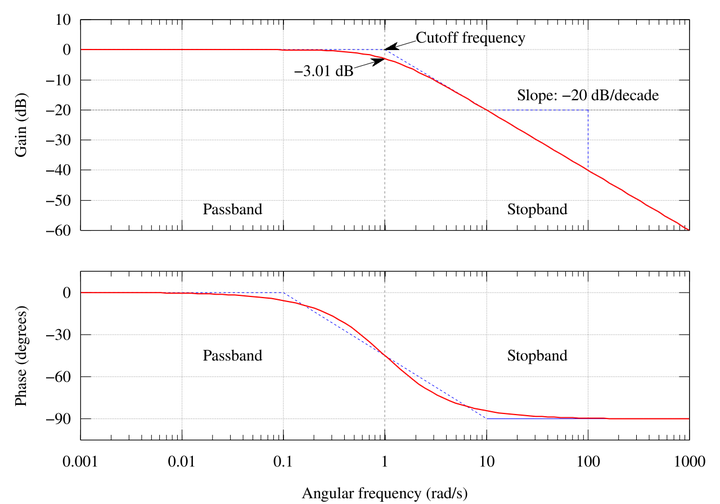
如果看不懂没关系，我们想要的效果是上面那张图在截断频率更低处增益尽量维持为 1，而截断频率更高处增益尽量趋近于负无穷 dB （可以理解为增益为 0）。现实中就是，我们希望他截断的部分斜率越陡峭越好。当然，这可以通过多个巴特沃斯过滤器的叠加来实现。

可是，问题来了，增益部分多叠一点是好，可是相位部分又有另一种说法了。

我们希望下面的相位部分，在截断频率之前越平越好，最好维持为 0。可是，即使在 0.1fc 处，我们也可以观察到相位出现偏移，而如果叠加过多的过滤器，那相位那部分的也会越来越陡峭。

我们可以通过再去叠加一个增益恒为 1，但是纠正相位的过滤器，可是这又会引入新的问题，那就是，这样的理想滤波器也不存在，只能通过联级结构，不同截断频率的全通滤波器实现近似的相位补偿。

所以究竟应该怎么办呢？既然接近奈奎斯特频率的附近会出问题，我们简单粗暴地把奈奎斯特频率提高，留下一个缓冲区不就好了？

那么为什么选择的是 44.1 kHz 呢？

这里面有多种原因。

早期的数码音乐，其实是通过一个 PCM (Pulse Code Modulation) 编码器存储在录像带上的。

当然这个 PCM 编码器也具有解码的功能。

这是因为，PCM 是数字化的音频文件，虽然理论上数字化的文件在复制过程中能够保持不会发生失真，但是他有一个极大的缺陷，就是需要的带宽比模拟信号要大得多。

录音机那种磁带带宽大概在 15 kHz ~ 20 kHz，但是录像带能做到 1 MHz ~ 1.5 Mhz，差不多高了一整个数量级，这是选择录像带存储数字音频的动机。

至于为什么是 44.1 kHz，那是因为使用这个频率不仅能够满足前面所述的各种要求，他同时也具有很强的兼容性。

在黑白电视普及的时候，视频一般分为 PAL 和 NTSC 格式。这二者的场频率分别是 50 Hz 和 60 Hz （正好跟所在国交流电频率吻合，不然会产生互调失真，反映在画面就是会有一个黑色的长条向一个方向滚动），最小公倍数为 300 Hz。

其中每一线可以容纳 3 个采样，所以采样率成了 900 Hz 的倍数。

PAL 信号同时激活的每一场的线数是 6 的倍数，而 NTSC 是 5 的倍数。

如果要求采样率高于 20 kHz，又不高于 PAL 支持的上限 46.875 kHz，如果想要同时兼容 PAL 跟 NTSC 标准，以下频率满足需求：

40.5 kHz, 41.4 kHz, 42.3 kHz, 43.2 kHz, 44.1 kHz, 45 kHz, 45.9 kHz 和 46.8 kHz。

其中，比 44.1 kHz （NTSC 为 44.056 kHz，即 44.1 kHz/1.001，这是 NTSC 制式从黑白转彩色时，因为技术缺陷导致需要额外的同步信号，所以画面的频率会降低）低的不能满足前面所述低通滤波器需要的额外频宽，而超过的数值又会影响同步信号。

最后经过混叠抑制，相位保真，以及硬件制造成本，数据储存以及传输成本上的取舍，工程师们选择了 44.1kHz。

所以最后 44.1 kHz 这个标准就保留下来了。一般情况下，CD 会使用 44.1 kHz 这个采样率。

当然，索尼 （$ONY）除了 44.1 kHz 16 bit 的标准，你还可以采用 。44.1 kHz 14 bit 的标准，然后留了 2 bit 做纠错码，牺牲一定的动态空间换取数据的完整性。

那为什么后来又变成 48 kHz 及其倍数了呢了呢？这边就简单提一下，权当抛砖引玉了。

首先，后面的数字音乐已经不需要古老的磁带机和 PCM 编码解码器了。48 kHz 比 44.1 kHz 相比，奈奎斯特频率更高一些，这样重建时可以使用一个更缓和的低通滤波器（这样失真也会更小，因为现实是不存在一个完美的低通滤波器的）。

算力和储存介质的革新也支撑突破 44.1 kHz 的限制。

更重要的是，48 kHz 与 44.1 kHz 不同，能够被常用的视频频率所整除，这样在进行音视频编辑的时候更加容易。

后期处理会使用 96 kHz 甚至更高的数字，那是因为很多后期的效果器，他的算法并非是线性的，使用更高的采样率才能避免出现混叠或者精度丢失的现象(举个例子，你录制一段音频，然后你通过直接拉长音频的方式降低音频的音调，48 kHz 甚至更高的采样率会给你更多的因为信号重建带来的噪音消除的的空间），不过输出最终使用的音频，其实 48 kHz 或者 44.1 kHz 就够了。