这是一个非常棒的问题，因为它必然会涉及到物理学中的许多不同领域——当我们开始讨论温度时，经典热力学自然会出场，而统计物理又会提供给我们一个不同的、基于微观层面的视角；而我们讨论温度的上限时，这往往会和能量极高的状态有关，因此必然无法避开相对论、粒子物理甚至有关量子引力的讨论。

首先我们必须给温度一个明确的定义。

温度的定义 经典热力学 绝对零度的存在

题主在题目描述中陈述：

温度是大量微观粒子无序运动的宏观统计值

这确实是温度的一个直观理解，但是这个“定义”过于模糊以至于难以明确计算和讨论。事实上，在经典热力学中，温度的定义依赖于内能和熵两个热力学量：

这里可以简单地理解为内能关于熵的变化率。^[1]其中内能和熵在经典热力学中可以被视为“公理化地”存在着的热力学量（当然统计物理中会有微观上的解释，后面我们再回到这一点）。

那么，出于数学上的考虑，温度既然是由微商这种类似比例式的形式定义的，其必然存在一个零点，也就是绝对零度。从实验角度考虑，经典热力学推导得到的热机理论让我们可以用传热和做功等能测量的量计算出任意两个系统的温度比值，因此只要我们定义某个系统的温度是 1，那么用比例就可以定义任意温度值（也就是得到了温度的单位），不难看出这里面零点“T=0”是比例意义上自动会存在的^[2]。^[3]

但为何我们常说“绝对零度不可达到”呢？这和由实验观察总结得到的热力学第三定律有关，其内容为：随着温度接近 0，等温过程的熵变也接近 0。

因此当温度高于 0 时绝热过程没法把温度降到 0，实际你会发现设计不出热力学过程在有限步骤内让温度降至 0。这也就是常说的绝对零度不可达到。

经典热力学理论并没有给温度的最高值一个限制。这本质上是因为热力学并没有规定内能和熵之间具体是什么函数关系，因此温度作为内能关于熵的变化率也没有太多的限制。

统计物理 二能级系统中的温度概念 温度与微观粒子的速度

在统计物理中，我们认为热力学系统就像是一堆粒子落在一系列能级上，因此内能就是总的能级乘以粒子数加和。熵被定义为：

Ω是系统处于此排布时可能的微观状态数（即给这些粒子编号，看有多少种方式排出来当前的能级分布）。因此我们也常说熵代表了“混乱程度”。

因此，如果我们讨论某些特定的模型——比如现在我们研究一下只有两个能级（设为 -ε和ε）的系统，那么熵和内能都是可以具体计算的，因此根据上面热力学中温度的定义，为了计算温度，我们需要考虑熵和内能的变化关系。只需作思想实验：

1. 当内能为 -Nε时（N 为总粒子数），对应着所有粒子都必须落在低能级上，因此显然只有这一种排布方式，Ω=1，S=0.
2. 当内能逐渐升高，少量粒子（设为 N0 个）分布在高能级上，从简单的组合学可以得知 ，因此熵也逐渐升高。
3. 当内能进一步升高至 0，即两个能级粒子一样多（即 N0=N/2）时，由上式可知熵达到最高。随着内能再上升，低能级粒子少于高能级，熵开始回落。
4. 内能达到最高 Nε时，所有粒子必须都在高能级上，熵为 0.

因此不难画出内能与熵的关系：

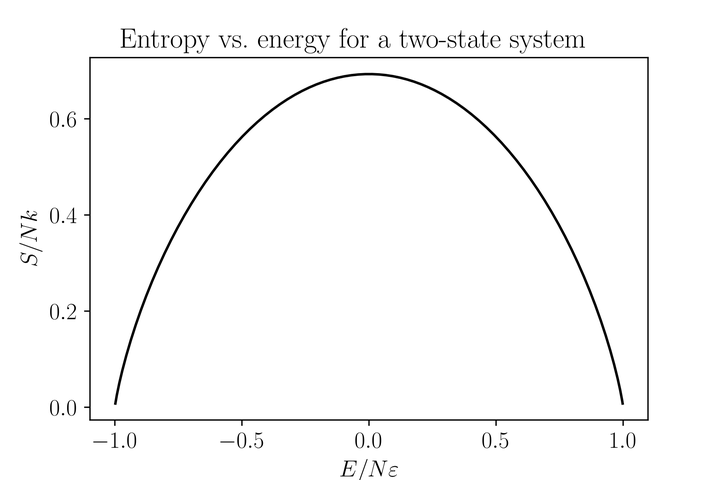
回忆定义，温度即为 S-U 曲线斜率的倒数，如下图：

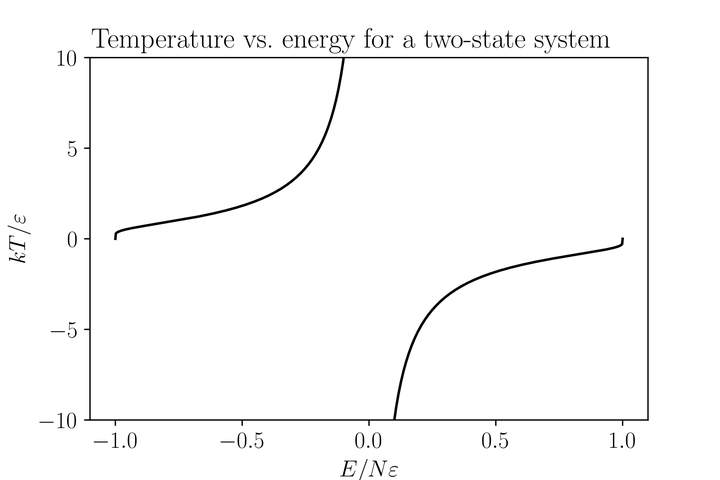
因此随着能量从最低开始升高，温度先从接近 +0 上升至 +∞，然后直接跳到 -∞开始下降，当能量达到最高时温度接近 -0。因此有答主指出温度的最高值是 -0。关于负温度更细致的讨论见：

如何让一种物质达到绝对零度以下？会发生什么？

这个解释确实在数学和物理上都很漂亮，但是实际很少有类似二能级系统这样，能级有最高上限的系统，因此负温度并不常见。例如，对于理想气体的模型来说就没有一个最高的能级。如果只考虑类似上述方法的计算，那么也不存在一个最高温度。

题主在问题描述中提出的困惑是，温度和微观粒子运动有关，既然粒子速度有上限 c，那么温度是否会有上限。事实上，我们可以考虑例如理想气体模型，限于篇幅这里直接给出结论：理想气体有着常数热容^[4]，因此温度和内能成正比。而模型中的内能由气体微粒的动能（包含平动、转动等）给出，而虽然运动速度存在着相对论上限，但速度接近 c 时动能是趋于 +∞的，因此动能没有上限，故而温度也没有上限。

粒子物理学 Hagedorn 温度^[5]

从前面统计物理角度的讨论我们知道，想要讨论温度的性质往往离不开具体的模型。根据粒子物理学的标准模型，强子物质（可以粗略理解为我们日常意义下的物质，不包含光子电子中微子等）似乎存在一个最高的温度，即Hagedorn 温度

（量级为

）。因为基于其能级模型，可以计算出想要达到这个温度需要无穷多的能量，并且温度高于

时模型没有有意义的解^[6]。

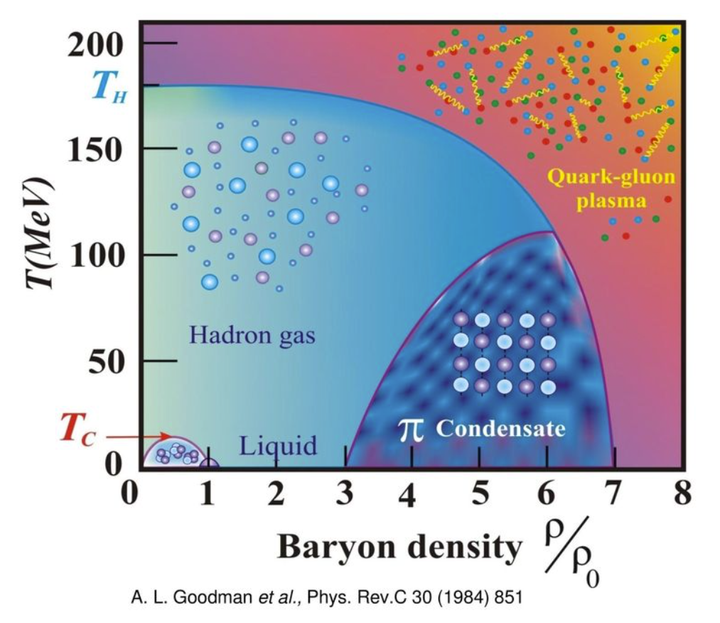
但这不应理解为严格意义的温度上限，可以认为接近这个温度时，强子物质会“相变”为一种夸克 - 胶子汤的状态，更高的温度仍存在，只是通常意义下的一切物质已经“解体”或“蒸发”了。熟悉相图的读者可以参看下图：

极高能量时的理论困难 量子引力

想必读者应该听说过普朗克长度的概念，这是由一系列物理常数拼凑出来的长度单位，从数学上看完全是为了计算美观得到的长度单位，其数值恰好相当相当小。从物理上看，若要研究这样小的尺度下的物理行为，经常不可避免地需要同时考虑量子效应以及引力的影响，而现在尚无成熟的量子引力理论，因此达到这一尺度会发生什么对物理学家来说是未知的。

回到温度的话题，根据电磁辐射的模型，温度极高时物体发出的热辐射会具有极高的能量，以至有着极短的波长。在普朗克温度的量级（约

）热辐射的波长会接近普朗克长度，因此讨论如此高的温度不可避免地需要量子引力理论。如果套用广义相对论的结论，如此高能的热辐射甚至会直接坍缩成黑洞。

实际上这和宇宙早期的情况非常类似，在大爆炸后一个普朗克时间内，宇宙的温度可能会高于普朗克温度，目前物理学家还没有弄清楚这段时间发生了什么。

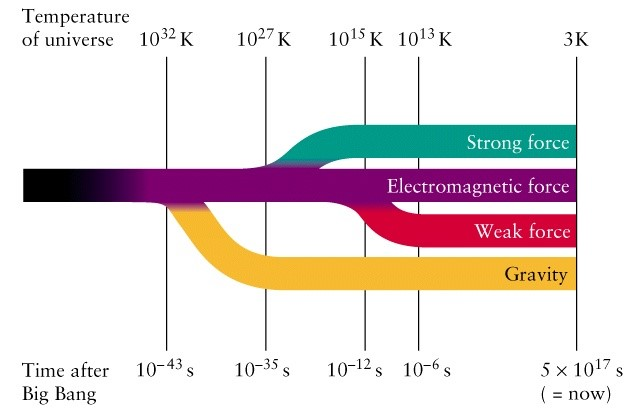
另外值得一谈的是，我们所有关于温度的讨论都要基于热力学，这些定义往往需要系统达到平衡态才有意义。而当粒子能量极高，动能极大时，系统是否能达到平衡态也是一个问题。只能说当我们考虑各种实际的因素之后，问题变得相当复杂和混乱。

至于最高温度的答案究竟为何，这取决于你想要采用哪个模型、关注何种意义下的“最高”，前述每个方面的讨论都可以视为一种不错的答案。