题主谈到的导线应当就是普通电线，普通电线流过它的额定电流时导线间的电动力是很小的。如果我们把导线换成导体，且题主的“通电导线”分别换成通直流电的导线和通交流电的导线，则题主的问题显然具有一定的工程运用价值。

基于此，我从工程运用的角度来回答这个问题吧。探讨中，我们把题主提问中的“导线”换成导体，如此一来，我们就可以对电气工程中大量使用的母线铜排或者铝排做讨论了。

我们这就开始。

注意 1：本帖不作理论探讨，仅提供具体的计算方法。如果要推究这些计算方法的来源，请参阅任何一本《电器学》、任何一本《高低压开关电器设计手册》，以及《工业与民用供配电设计手册》第四版。

本帖主要讨论平行导线的电动力。至于垂直导线的电动力，请参阅本帖后部的教材截录，其中有专门内容，可供参考。

1.关于直流电流通过导体后，导体间产生的电动力计算方法

我们看下图：

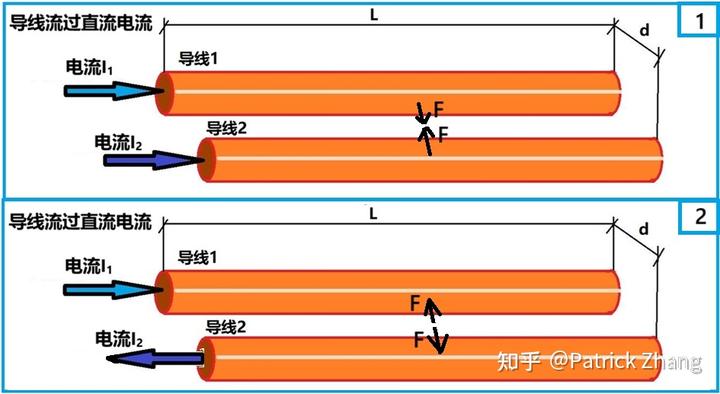
对于图 1 的 1 图，两导线的电流方向相同。我们用右手螺旋定则判断磁力线方向，再用左手定则判断电动力方向，我们发现两导线之间的电动力是吸力；对于图 1 的 2 图，两导线的电流方向相反，我们用右手螺旋定则和左手定则判断电动力方向是斥力。

由毕奥.萨法尔定律可知，两导线之间的电动力表达式为：

式 1 中，F 是电磁斥力，单位是 N；μ0 是真空磁导率；I1 和 I2 是两导线中的电流，单位是 A；L 是导线长度，d 是导线中心距，L 和 d 的单位均是 m。

举例：如果两导线流过 10A 的直流电流，且电流方向相反。又知导线的长度是 5m，导线中心距是 5cm，求两导体之间的电动力。

我们把数据代入到式 1 中：

我们看到，此导线间的电动力是 0.002N，很小。

在工业的供配电系统中，导线中的电流再大也大不到哪里去。电流相对较大的是开关设备中的矩形截面母线，电流一般在数百安到数千安。如果发生了短路，则短路电流可达数十千安到一百多千安。

注意 1：此时导线的称谓必须换成导体或者母线了。

我们看下图：

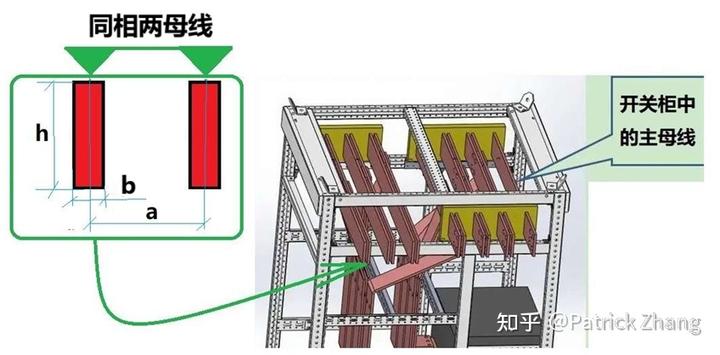
我们从图 2 看到，主母线铜排具有一定的厚度 b 和宽度 h，其截面积 S=hd。注意到同相两母线铜排流过的交流电流方向是一致的，而不同相铜排流过的交流电流存在相位差。

我们看下图：

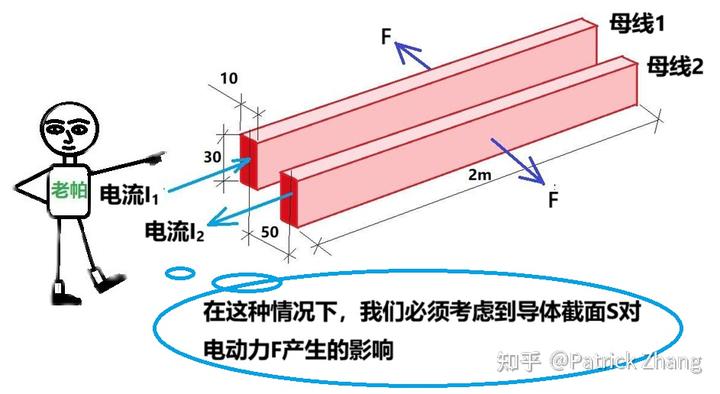
注意：图 3 中的数值单位均为毫米。

为此，计算电动力的式 1 要添加截面系数 Kc，如下：

式 2 中的截面系数 Kc 如果来实际计算，其计算式比较复杂。在工程中采用图表计算法，图表见下图：

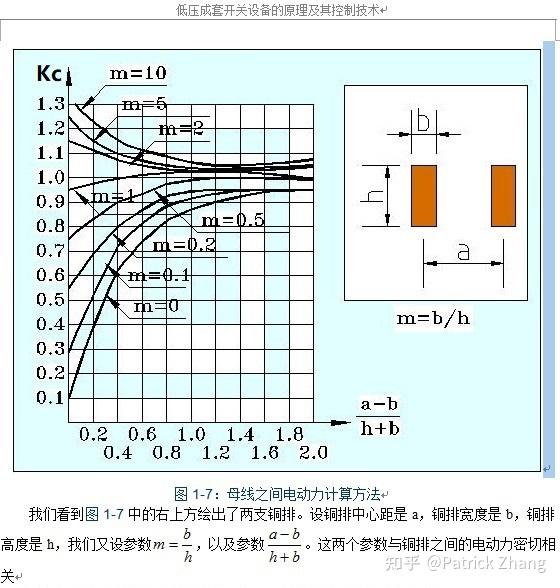
我们按图 3 来计算截面系数，计算时的数值单位均为毫米：

图 4 中没有 m=0.3 的曲线，我们就以 m=0.5 和 m=0.2 的中间位置来考量。我们从图 4 中横坐标 1.0 往上看，在 m=0.5 和 m=0.2 的中间位置向左侧看纵坐标，Kc≈0.95。

如果图 3 中母线流过的直流电流均为 500A，且母线长度 L=2m，中心距 d 也就是图 4 中的 a=0.05m，我们按式 2 来求电动力：

看得出来，电动斥力 F=1.9N 对于铜排稳定性来说就等于隔靴搔痒，毫无影响。

2.再看交流电流下的导体间电动力

我们知道交流电分为单相交流电和三相交流电，而电流又分为运行电流和短路电流。以下，我们分别来讨论。

（1）单相交流电下的导体间运行态电动力

我们把式 2 中的电流 I1 和 I2 换成交流电流 i1 和 i2，再把式 2 改写为：

这里的

，其中 Im 是电流幅值，I 是电流有效值，ω是电流的角频率，t 是时间。

当 i1=i2 时，式 3 为：

我们把 Fh 叫做交流电动力的恒定分量，又叫做交流电动力的平均力；把 Fj 叫做交流电动力的交流分量，注意到其幅值等于平均力，但频率为电流频率的 2 倍。

我们看下图：

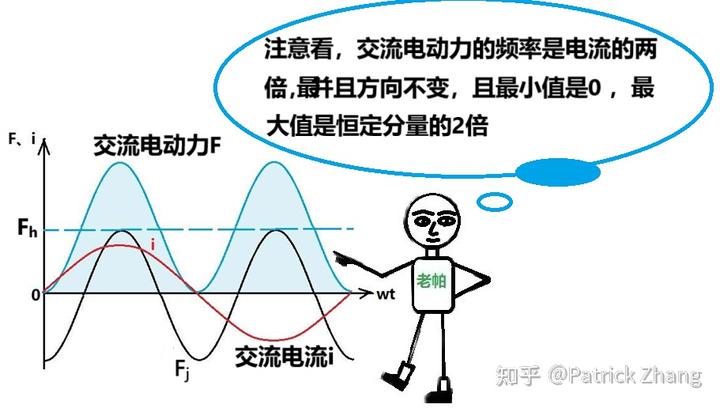
（3）三相交流电下的导体间运行态电动力

我们设流过三相母线的电流分别为：

。

我们看下图：

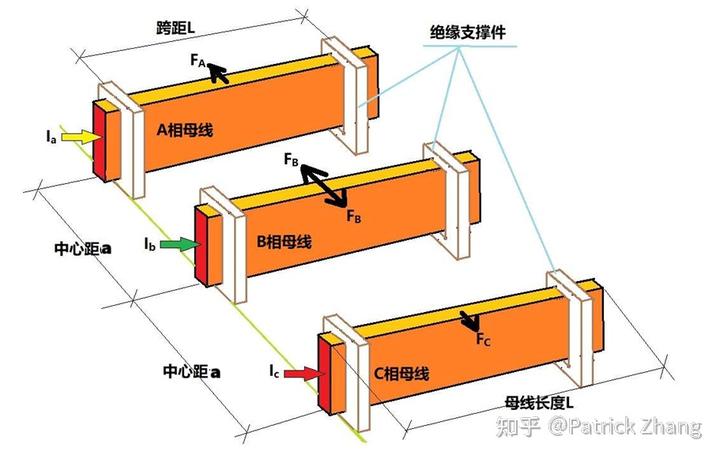
我们看到 A 相母线和 C 相母线所受到的合力是向外的推力，而中间相 B 相母线受到的力是来回摇摆的力。

我们先看 A 相母线受到的力：

经过变换化简后得到：

为了求得最大值，我们零

，由此得到

，由此得到 ：

，或者

我们把它代入到 Fa 的表达式中，得到：

用类似的方法，我们会发现 C 相母线的受力与 A 相母线受力完全对称。

对于中间的 B 相，用类似的方法得到：

可见，中间相母线的受力是最大的。

（4）三相交流电下的导体间短路态电动力

当三相平行直列导体（母线）发生三相短路时，短路电流为：

，

对于配电网，一般来说

，故可推得 A 相和 C 相受到的最大短路电动力是 -2.65F0，中间 B 相受到的最大短路电动力是±2.8F0。

我们来看一个例子：

设某开关设备中的主母线采取直列排列，长度为 10m，母排中心距是 0.35m。设冲击短路电流峰值为 40kA，求中间的 B 相母线受力。

第一步：

第二步：设截面系数 Kc≈1

第三步：求中间 B 相母线的受力

我们看到，短短的 10 米长度母线，其中间相就受到 2.612 吨力，可见短路电流的破坏力有多大。

4.通过截录教材内容来解答题主的垂直导线电动力的问题

郭凤仪《电器基础理论》中的相关内容摘录：

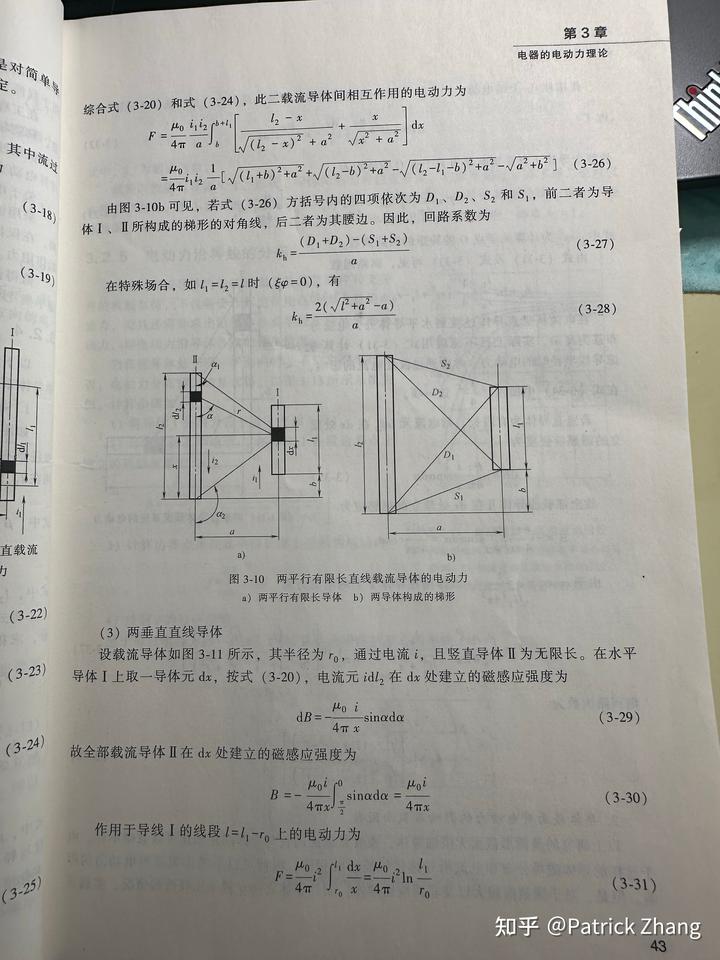
图 9 和图 10 专门回答了垂直导线电动力的问题。

另外，我们看到，工程运用中的导线电动力计算方法与物理教材中的计算方法存在一定的差异。对于题主的问题来说，最大差异就是截面系数 Kc。

就写到这里。