电子和声子如何相互作用形成电荷密度波的?

正好是做这个的,就来回答一下。
@
已经以一维体系为例很好地解释了电荷密度波的Peierls 机制。由于电荷密度波这个想法就是 Peierls 提出的,无论在教科书上,还是实际材料中,讨论电荷密度波首先就要考虑这个机制。
不过,这个机制的核心并不是电子声子耦合(electron-phonon coupling)。从@
给出的这个公式 中可以看到,当式子中的q接近
时,式子右边的分母无穷小,于是右边那一项的值就趋于无穷大。在这种情况小,不管电声耦合强度
有多大,式子的值都将小于 0,使得 instability 出现。其实,@
没提到的一点就是,
实际上就是 1 维体系的费米面嵌套矢量(Fermi surface nesting vector)。因此,在这种机制中,电荷密度波来源于费米面的 nesting。在研究中提到这种机制(Peierls 机制),人们常常会称之为Fermi surface nesting 机制。不幸的是,这种机制不足以解释很多真实材料中发生的电荷密度波现象[1]。而还有一种机制,叫做 “q-dependent electron-phonon coupling induced period-lattice-distortion”机制(与 q 矢量相关的电声耦合导致的周期性晶格畸变机制)。这种机制中起决定性作用的,就是电声耦合了。下面我简单介绍一下电荷密度波以及这两种机制。
一、什么是电荷密度波(charge density wave,CDW)
为了让大家对电荷密度波这个东西有一个直观的认识,我先给大家看两幅图。 下面的图 1 是典型的电荷密度波材料 1T-TaSe2 中的电荷密度波畸变的示意图。在未发生电荷密度波相变时,TaSe2 中的 Ta 原子彼此距离相同,原来的晶胞是图中那个较小的发亮的菱形。而发生了电荷密度波相变后,原子位置发生了畸变,形成了一个一个被称为 David star 的六角星结构。这种结构也具有周期性,对应的新的晶胞就是图中的大菱形。
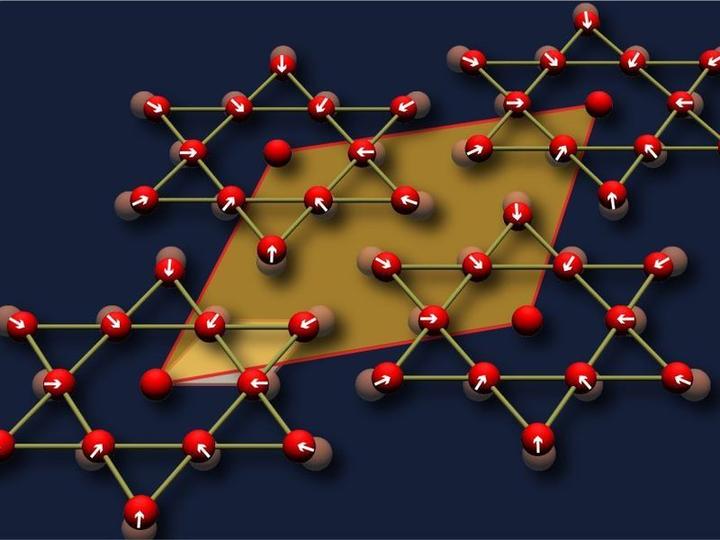
图 1: 1T-TaSe2 中的电荷密度波相中的晶格畸变示意图
不过,电荷密度波的核心在于周期性的电荷密度调制(charge-density modulation)。它应该是这样的:
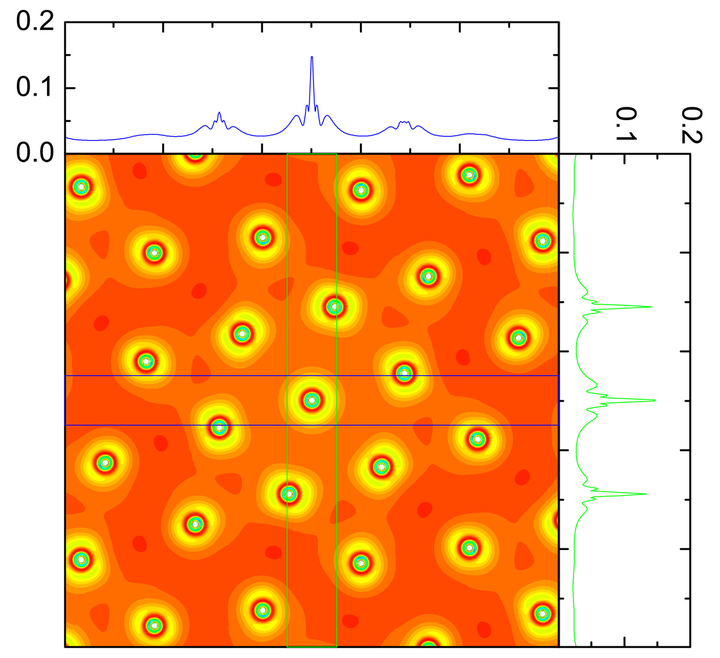
图 2: 1T-TaSe2 中的电荷密度波相的电荷密度示意图 [2]
二、费米面 nesting 机制(Peierls 机制)
这部分内容在很多教科书里都能看得到,前面@
也给出了理论解释,我这里从图像上(不严谨)地描述下。
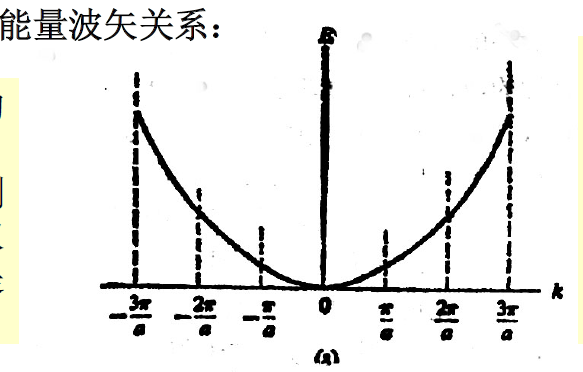
图 3:在倒空间中,电子的能量随波矢的变化关系可以用一条开口向上的抛物线来描述。
我们假设有一个电子处在一个一维的空间中,电子的能量可以表示为
,其中
是倒空间的矢量。如果把电子从
到无穷的能量变化画出来,就可以得到一条开口向上的抛物线。
不过,实际上的材料并不是这样的一个空旷无限的空间,而是一个一个完全相同的基本结构单元(这种基本单元被称为晶胞)拼接堆垛而成(这被称之为平移对称性)。假设有一条一维单原子链,链上相邻原子间的距离为
,这条单原子链就可以被看成尺寸为
的基本单元重复而成。任意取一个原子为坐标原点的话,在倒空间中,这个基本单元被定义为
到
之间的部分,尺寸为
,如图 3 所示。
根据平移对称性,每个能量单元之中电子的能量变化都应该一致,这样的话在空间中电子的能量情况就变成了下面这样,很多完全相同的抛物线交织在了一起。。。
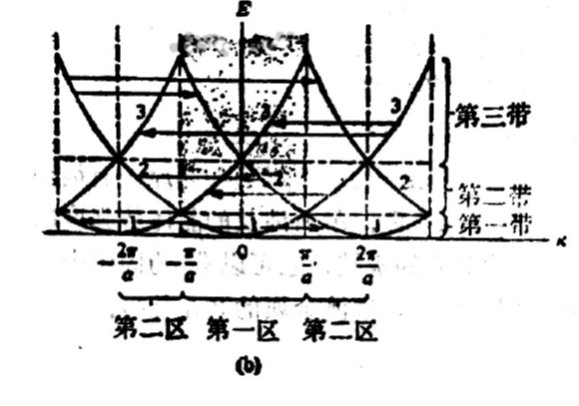
图 4:电子的能量随波矢的变化可以用抛物线来描述。根据平移对称性,无数完全相同的抛物线交织在了一起。
这样交叉在一起的抛物线把人都搞混了好吗!比如晶胞边界
处,相邻的两条抛物线交叉,有了一个交点。电子走到这里的时候,是朝上走还是朝下走呢??
为了解决这个问题,物理学家们说:“duang!我们来加特效!”于是他们考虑了周期势场的影响,把原来的抛物线画成了这样:
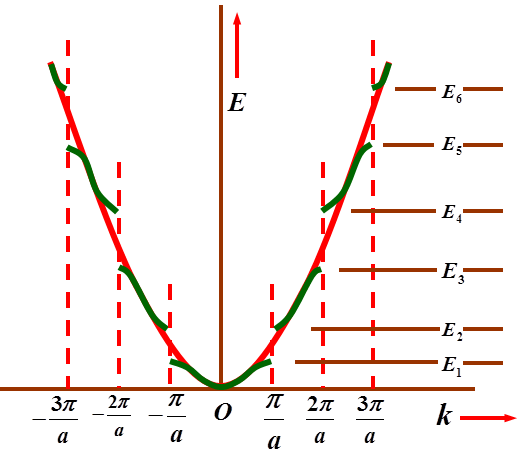
图 5:在周期势场的作用下,虽然电子的能量分布仍然基本保持抛物线的形状,但在布里渊区边界处,原先相互连接的部分,现在分开了,出现了一个能隙。
在这条抛物线上,仍然保持连接的部分,就被称之为能带(band)。而中间被打断的部分,被称之为带隙(gap)。我说了这么多,是希望大家记住一点:在布里渊区边界处,能带会打开一个 gap。
当年 Peierls 一个人瞎琢磨,他假设了一条一维单原子链,链上的原子均匀分布,每个原子上有 1 个电子。体系是半满填充,费米能级位于
处,而布里渊区的边界位于
处。
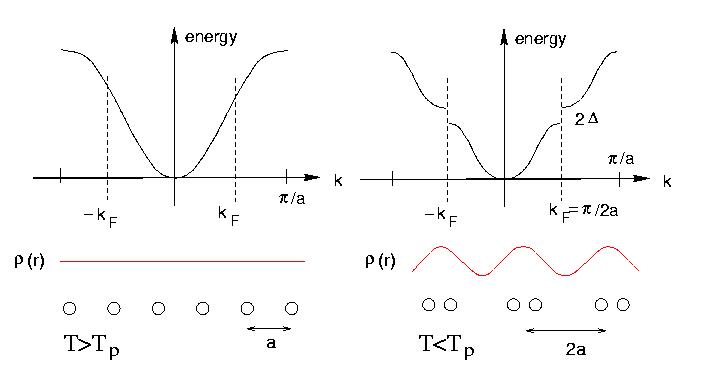
图 6:晶胞长度为的一维单原子链半满填充,费米能级位于能带中间,体系保持金属态(左图);当发生二聚化后,晶胞长度变为
,对应的布里渊区缩小,边界变为
,打开一个 gap。此时费米能级位于 gap 内,体系进入绝缘态(右图)
Peierls 说:“给这个原子链一点点微小的扰动,让它们两两靠近一点,duang!”这个时候,晶胞的长度就变成了
,使得原来的
变成了布里渊区的边界,这样就打开了一个 gap。根据能带理论,费米能级位于能带内,体系就是金属;位于 gap 内,体系就是绝缘体。所以,在原子链上的原子发生了二聚化畸变后,体系由金属变成了绝缘体。
Peierls 掐指一算,发现这种二聚化后的状态能量竟然比原来要低,这意味着这种态可以稳定存在。 于是,电子密度在这一新的周期场中重新分布,被命名为电荷密度波;而这种相变,被命名为 Peierls 相变。
考虑更加普遍的情况,如果每个原子平均提供任意价电子数,畸变晶格的晶格常数
将不一定为
。由于费米波矢
与第一布里渊区边界重合时使得体系能量最低,新的晶格常数仅取决于费米波矢
,与原来的晶格常数无关。可以看出,Peierls 不稳定性与一维体系布里渊区边界和费米面形状的几何特点有直接关系。一维体系的费米面就是
空间中两点(抛物线中
处),位于
处的费米面以长度为
的矢量进行平移后,能够与位于
处的费米面完全重合。这种费米面的平移一个特定矢量后能够与另一处的费米面完全重合的情况就被称为费米面嵌套(Fermi surface nesting),而这个平移矢量就被称为嵌套矢量(nesting vector)。将这个矢量
转化到实空间,就可以得到畸变晶格的晶格常数
。这就是@
在答案中提到的
这个矢量的由来。
上面的描述是图像性地定性描述,相当于从结果倒推原因。不过,既然已经找到了Peierls 机制的驱动力
,理解@
的答案就比较容易了。
对于构成材料的原子,我们也可以像画电子能量分布图一样,画出晶格振动(被称之为声子)频率随着
矢量的变化关系。Kohn 指出:对于一维金属,声子的振动频率在
处会显著降低并且不再连续,这就是@
提到的 Kohn 异常[3]。
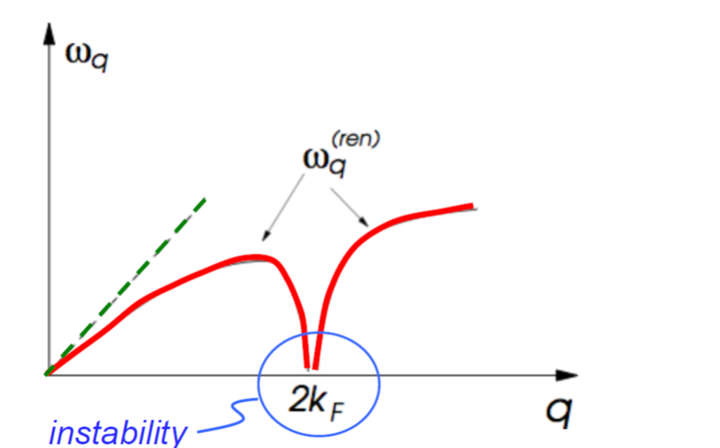
图 7:对于一维金属,声子的振动频率在处会显著降低并且不再连续.
声子的振动频率本来应该是实数(在图 7 的纵轴正半轴),当声子的振动频率变为虚数(在图 7 的纵轴负半轴)时,你能想象,材料肯定出了什么问题了。这样的虚数频率(虚频)暗示着相变的出现。对一维体系,Kohn 异常导致在费米面嵌套矢量处出现虚频,对应着晶格发生畸变,产生周期为
的周期性原子位置和电荷密度的再分布。这就是解释电荷密度波的费米面 nesting 机制(Peierls 机制)。
费米面 nesting 机制(Peierls 机制)能够解释一些一维材料的电荷密度波特性,但对二维和三维材料中出现的电荷密度波现象,这种机制似乎就不足以解释了。
三、电声耦合导致的周期性晶格畸变机制(q-dependent electron-phonon coupling induced period-lattice-distortion)
在二维和三维情形,布里渊区的边界分别由直线或平面组成,而费米面则分别为曲线或曲面,只能和布里渊区边界相交或相切,不能完全地相互重合。此时费米面的 nesting 情况可以通过电子磁化率的实部:
和虚部
来反映。在 nesting 矢量处,电子磁化率的实部和虚部都应该有极大值 [1]。
而在二维或三维情况中,@
提到的公式就变成[4]:
(1)。
可以看到,上面式子(1)的右半部正是电子磁化率的实部
。如果一个电荷密度波材料满足费米面 nesting 机制,则在 nesting 矢量处式子(1)中的右半部会趋于无穷大,使得材料在该处发生电荷密度波相变。换言之,这种机制要求材料的 nesting 矢量必须和电荷密度波的矢量相同。
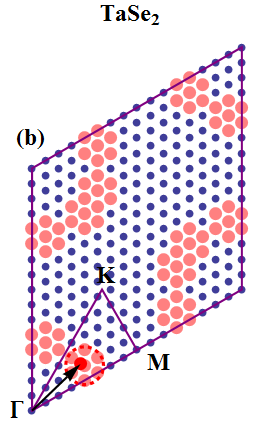
图 7:理论计算得到的 1T-TaSe2 的虚频分布情况[5]。黑色箭头和红色实心圆圈标出了实际的电荷密度波矢量。可以看到,虚频模式确实位于电荷密度波矢量处。
可惜,在真实材料中的情况常常不这么简单。以 1T-TaSe2 为例,通过密度泛函理论计算得到的其虚频的模式刚好位于电荷密度波矢量周围,而电子磁化率的实部和虚部反映出来的 Nesting 矢量却和电荷密度波矢量不一致[5]。这就说明,费米面 nesting 机制并不能解释这个体系中的电荷密度波特效。
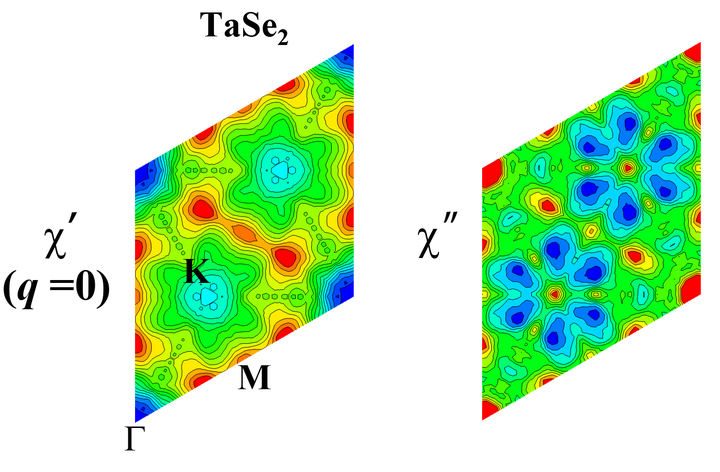
图 8:理论计算得到的 1T-TaSe2 的电子磁化率的实部和虚部[5]。红色的极大值对应的 nesting 矢量并不位于电荷密度波矢量处。
另一方面,如果式子(1)中的电声耦合矩阵元足够大,也可以导致虚频的出现,使得材料发生电荷密度波相变。 计算得到的声子线宽(反映了电声耦合强弱)
显示电荷密度波矢量处电声耦合很强。这就暗示着,电声耦合是这个体系中产生电荷密度波的主要原因。
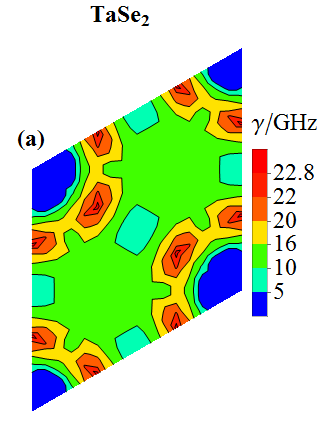
图 9:理论计算得到的 1T-TaSe2 的声子线宽[5]。在电荷密度波矢量处声子线宽出现了较大值。
四、总结
总的来说,式(1)中的极大值到底是来源于费米面 nesting,还是来源于电声耦合矩阵元
,就是这两种机制的区别。目前,至少在二维体系中,学界倾向于认为是电荷密度波的来源是电声耦合导致的晶格畸变,而传统的费米面 nesting 机制(Peierls 机制)顶多起一个次要的辅助的作用;但对于一维电荷密度波材料,在它的 nesting 矢量与电荷密度波矢量一致,此时就不知道费米面 nesting 和电声耦合矩阵元哪一个起主要作用了。因此,电荷密度波的起源,还需要进一步的澄清。
=======
参考文献:
[1]Fermi surface nesting and the origin of charge density waves in metals
M. D. Johannes and I. I. Mazin,Phys. Rev. B 77, 165135
[2]Orbital density wave order and electronic correlation driven insulating 1T-TaS2 monolayer
Xiang-Long Yu, et al.
http://arxiv.org/abs/1407.1407
.
[3] Image of the
in the vibration spectrum of a metal
W. Kohn, Phys. Rev. Lett2, 393 (1959)
[4] Effect of dimensionality on the charge-density wave in few-layer 2H-NbSe2
Matteo Calandra, I. I. Mazin, and Francesco Mauri, Phys. Rev. B 80, 241108(R)
[5] Nature of charge density waves and superconductivity in 1 T− TaSe 2−x Te x
Y. Liu, D. F. Shao, et al., Phys. Rev. B 94, 045131 (2016).