省流：最优解是 2，715 种组合中除了(1, 1, 1, 7), (1, 1, 1, 8), (1, 1, 1, 9), (1, 1, 1, 10), (1, 7, 10, 10), (2, 5, 7, 10)之外的709 种组合均有解。24 则在 566 种情况下有解。最差解是 97，只有 85 种情况下有解。

自然数 1-100 对应的可解的组合数如下图所示，横坐标为指定数字 X，纵坐标为有解的组合数。

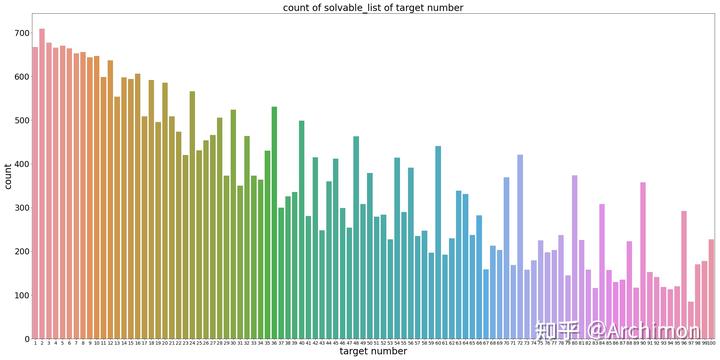
实际上我们还可以进一步定义每个自然数的『计算难度』。我们可以将其定为每个组合使用随机计算方式随机计算顺序尝试出正确解法的平均次数。这一计算难度实际上有解组数相反：平均计算组数最大的目标数字为 97，平均需要 3915.5 次才能尝试出一个正确的解法；而最简单的 2 则只需要 295.4 次即可。与这一数据由下图给出：

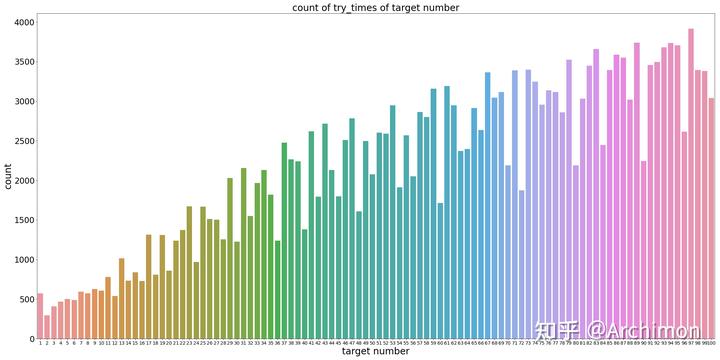
最差解 97 对应的 85 种有解情况及对应解法(每个组合仅展示一种解法)如下图所示：

本题可以重复，所以组合方式与不可重复的情况^[1]不同。这里的组合方式有 715 种，分别如下：

• 4 个不同数字的组合有 ，即 210 种；
• 3 个不同数字的组合有 种，即 120 种，
• 每种选取一个数字重复有 3 种方式，总计 360 种；
• 2 个不同数字的组合有 种，即 45 种，
• 每个数字出现 1 次，2 次，3 次 3 种情况，总计 135 种；
• 1 个数字构成的组合有 10 种

总计 210+360+135+10=715 种情况(当然也可以使用隔板法求解)。

接下来我们只需要遍历不同的计算方法和计算方式即可。核心还是基于二叉计算树遍历所有计算顺序。当然由于遍历情况较多最好开个多线程。进而获得每个自然数对应的求解方式，以及有解的组合。核心代码如下以下回答中所示：

1、2、3、4、5、6、7、8、9、10 这 10 个数字中任取 4 个不同的数，用加减乘除都能算出 24 吗？

具体来说，如最受关注的 24，在本题限定条件下的求解方式有：

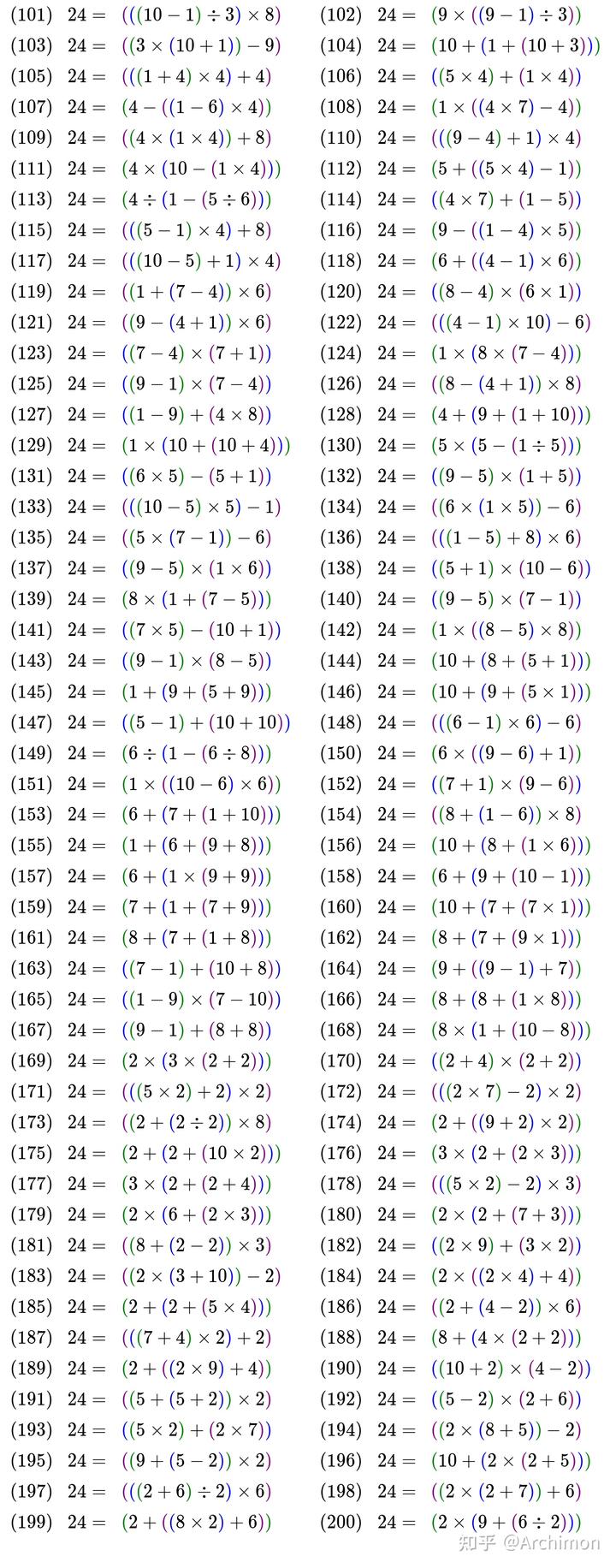
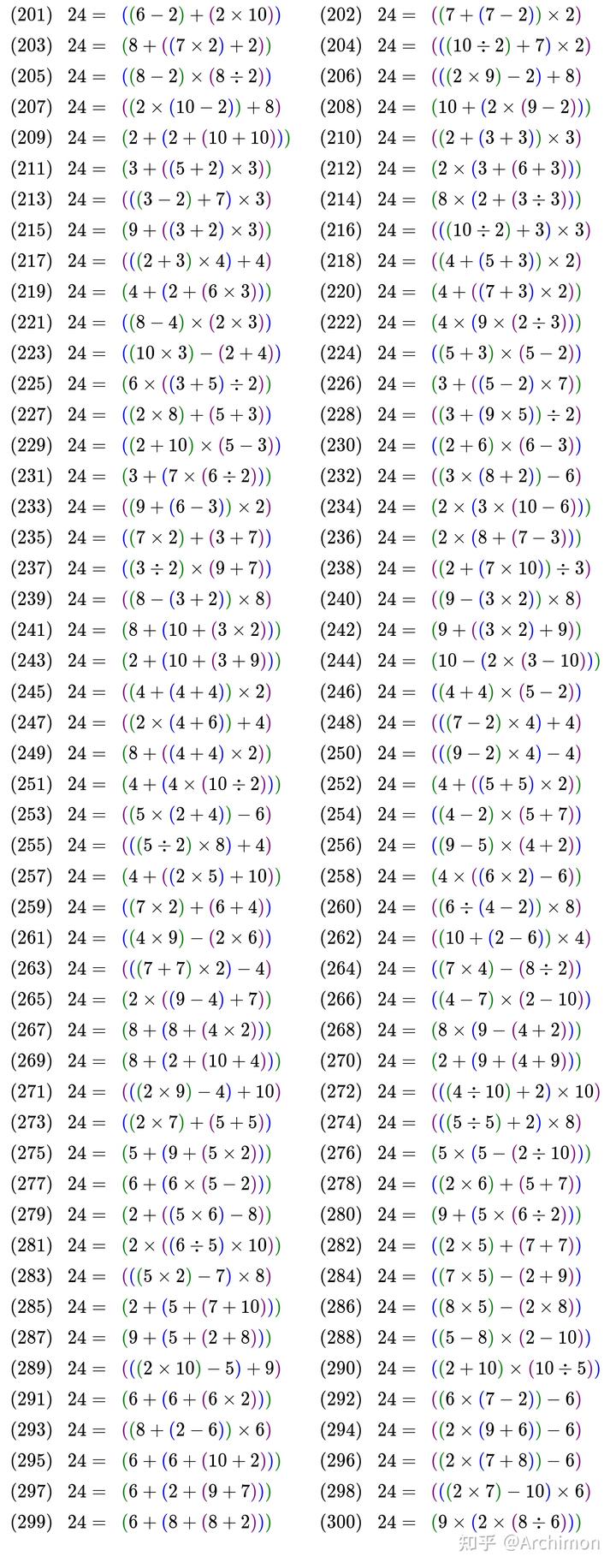
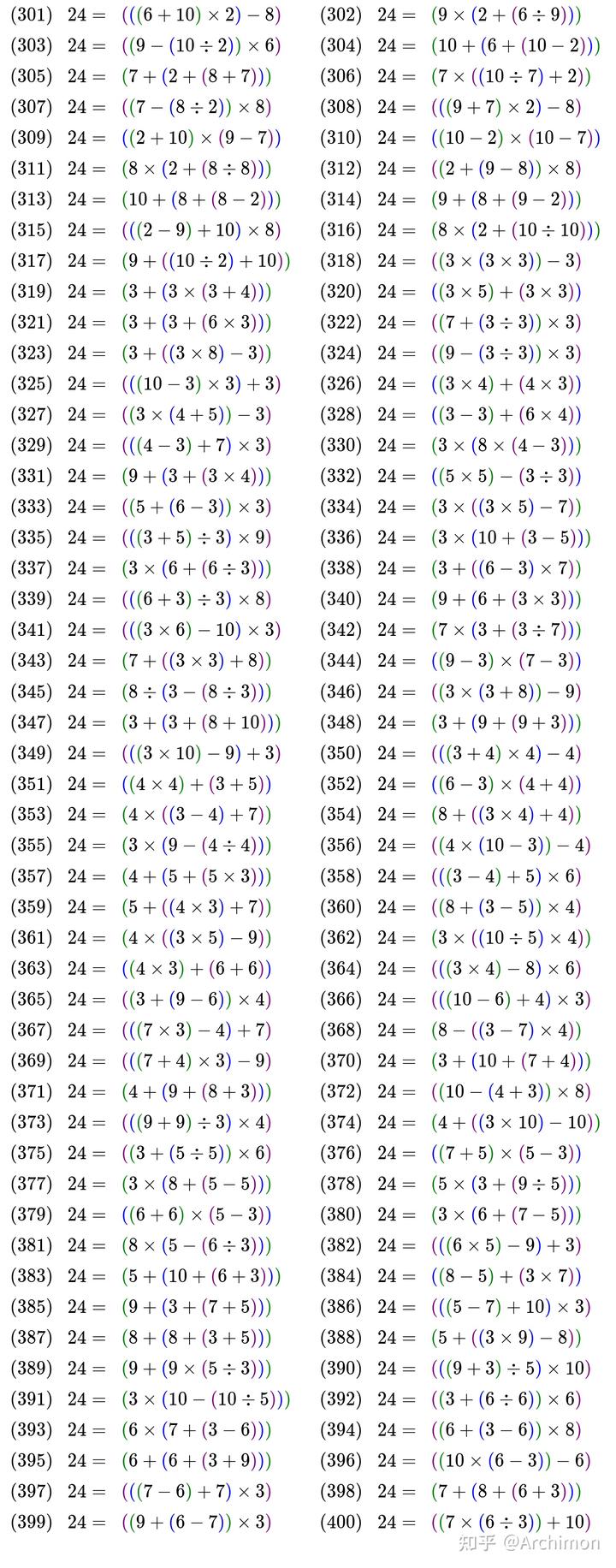
如果大家好奇含 JQK 的 24 点的完整解法，可以参考以下结果，其中 X 代表 10,J 代表 11,Q 代表 12,K 代表 13

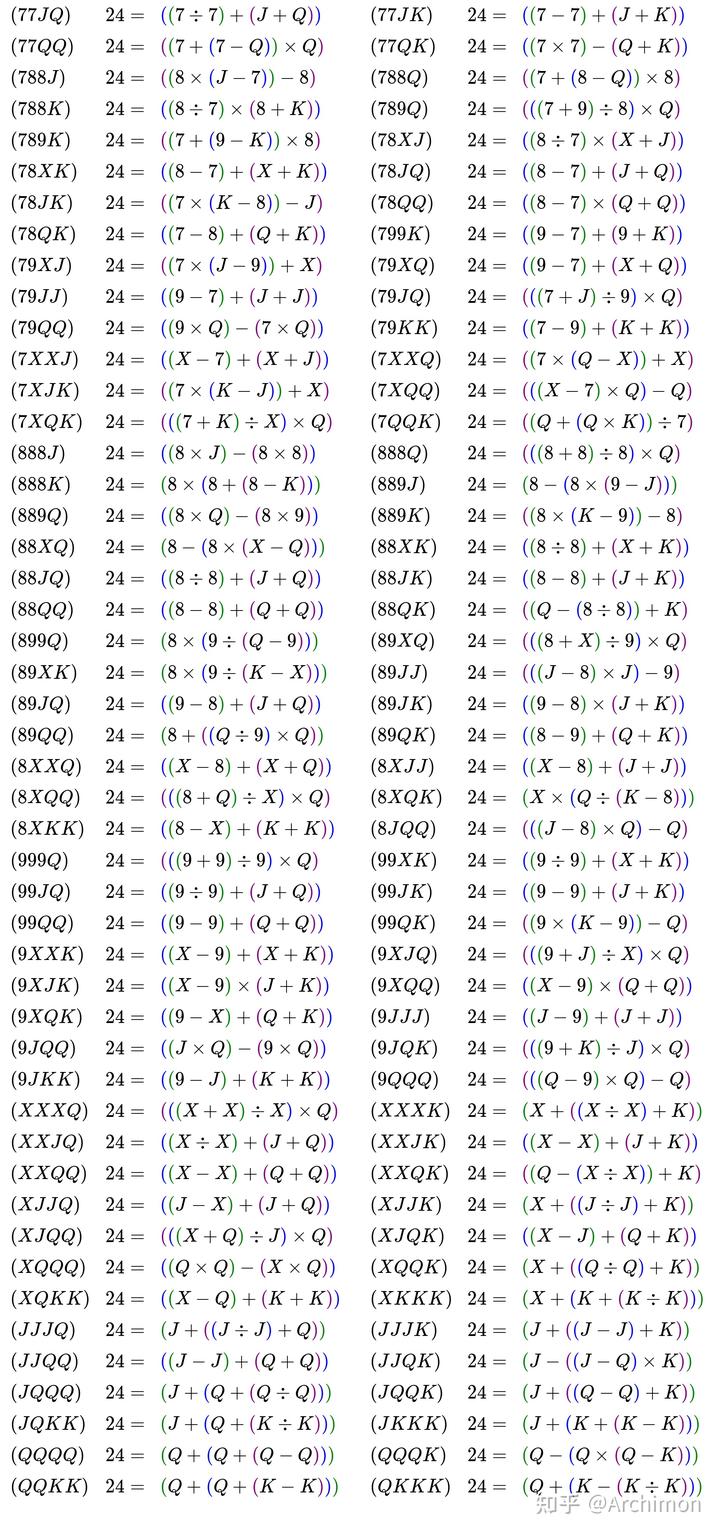
同样，此时也存在着一些引入乘方后才有解的组合，关于这类组合以及求解方案，可以参考：

第 881 题 有没有一些用正常方法解不出 24 点的四个数字？