古人很早就认识到地球是个球体。

不仅如此，还算出了地球的大小，甚至算出了月球和太阳的大小、地日距离和地月距离。

古希腊人首先注意到，远去的帆船逐渐消失在地平线下，桅杆是最后消失的，这种现象只有将海面看成是曲面才能够说得通。

他们还认识到，月食是因为地球在月球上投下了影子，但投下的影子是圆弧状的，这也表明地球是一个球体。

他们还知道，在南北不同纬度上的人们，所看到的星空是有差别的，如果地球是球体，就能很好解释这一点。

同样重要的事实是，每天抬头所见的太阳和月球本身就是圆的，这似乎表明球体是一种自然状态。

古希腊人还听说，在遥远的北方人们一睡就是半年的时间。这说的正是极夜现象，如果大地是球形的，那么球面上不同纬度就会有不同的白昼时长。

这些都让古希腊人足以相信地球是球形的。

我们接着说古人如何测出地球的大小。

测量地球这一壮举由埃拉托色尼完成。他了解到，在埃及南部的塞伊尼城附近，有一口特殊的井，每年的 6 月 21 日的中午，太阳会直射井底。

埃拉托色尼认识到，在这天正午，太阳必定在头顶正上方，今天我们知道，这是因为塞伊尼城位于北回归线附近。而这种事情却没有在赛伊尼北方的亚历山大发生过。

太阳不能同时在塞伊尼和亚历山大都处于正头顶，也说明大地是弯曲的。

埃拉托色尼由此想到了一个测量地球周长的方法。

夏至日正午，阳光直射塞伊尼井底。而在亚历山大，埃拉托色尼在地上立了一根直杆，通过直杆投下的影子，可以测量阳光与立杆之间的角度。

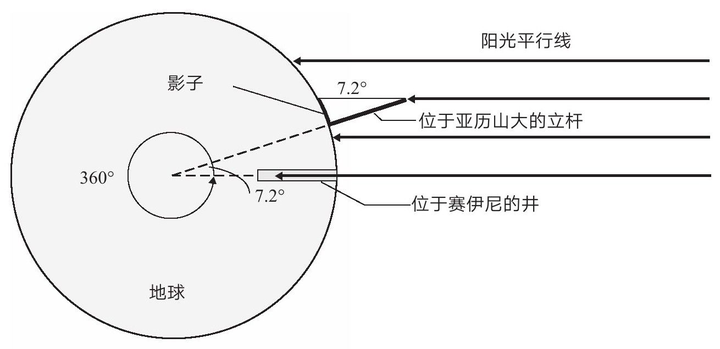
最关键的是，这个角度实际上等于亚历山大和塞伊尼两地到地球中心的夹角。他测出的角为 7.2°。

如果塞伊尼与亚历山大的夹角是 7.2°，那么塞伊尼与亚历山大之间的距离就是地球周长的 7.2°/360°＝1/50。

也就是说，知道了塞伊尼与亚历山大的距离，再乘以 50，就可以算出地球的周长！

埃拉托色尼算出的地球周长是 250000 斯塔德。一个斯塔德就是体育比赛用的跑道长度。当时奥林匹克体育场的跑道是 185 米，所以埃拉托色尼算出的地球的周长是 46250 千米，这仅比地球的实际周长大了 15%。

事实上，埃拉托色尼可能算得更准确。因为埃及人的一斯塔德只有 157 米，这样算出的地球周长是 39250 千米，误差只有 2%！

当然，这也得益于埃拉托色尼的运气不错。

今天我们知道，亚历山大并不在塞伊尼的正北方，它们在经度上有 3°的差距。夏至日的正午，太阳也不会完全直射塞伊尼，有 0.4°的偏差。而这两个误差恰好部分的抵消了。

我们再来说古希腊人如何测量月球太阳的大小，天体之间的距离等等。

有了地球的大小，就可以测出月球的大小。

部分工作已经由喜恰帕斯完成，他通过月食发生的时间，测出了地球的直径是月球直径的 4 倍。原理也很简单。

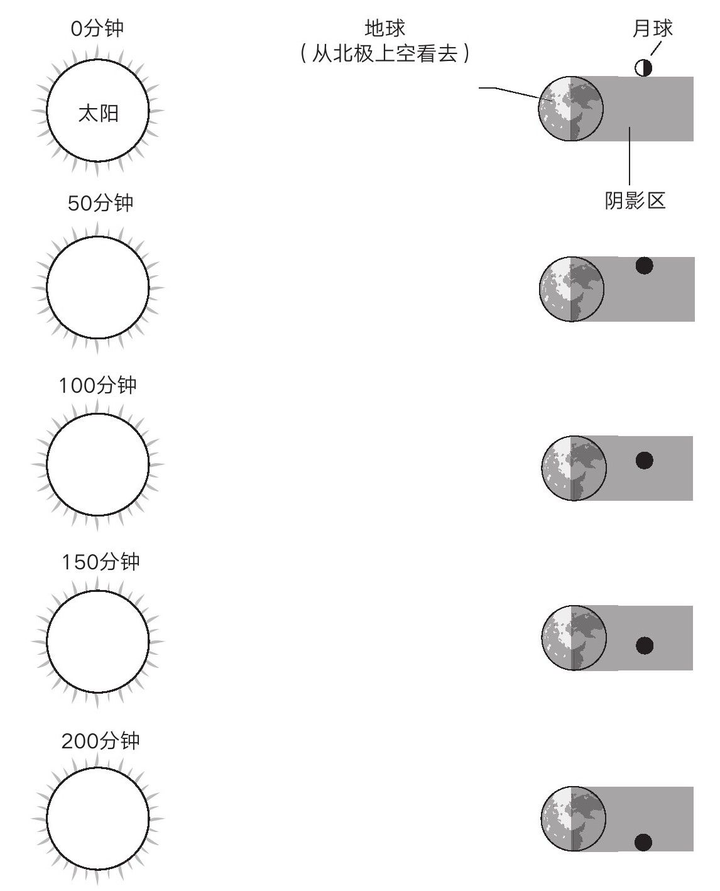
他注意到，月球从刚刚发生月食，到完全被遮挡，差不多是 50 分钟。而从完全被遮挡到月食完全消失，差不多是 200 分钟。这意味着地球的直径是月球直径的 200/50=4 倍。

现在埃拉托色尼算出了地球的大小，自然也就可以知道月球的大小。

地月距离很好估算，埃拉托色尼是这么做的：

将手伸到合适的长度，指甲盖就可以刚好遮挡月亮，指甲盖长度与手臂长度之比，就等于月球直径与地月距离之比。当然这样的误差会比较大，但已经可以算出地月距离。

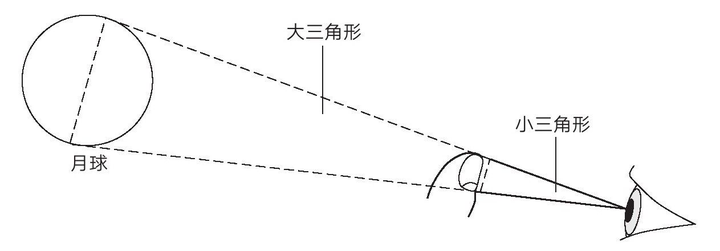
有了地月距离又如何算出地日距离？

这部分工作由阿里斯塔克斯完成，他相信月光是反射的太阳光。他接着论证道，如果真是这样的话，当地球，月亮，太阳形成一个直角三角形，那么就会出现半个月亮。

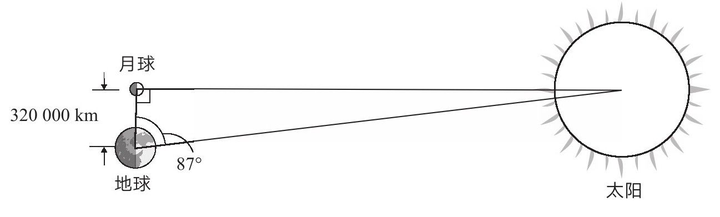
如果我们在半月的时候测出了地球与太阳之间的夹角，利用三角学和已经测得的地月距离，不就可以算出地日距离了吗？

阿里斯塔克斯测出的夹角是 87°，所以他算出地日距离是地月距离的 20 倍。

但实际上这个角度应该是 89.85°，实际距离是 400 倍。

这个误差已经非常大了。但重要的不是误差，而是找到了一种测量宇宙方法。

有了地日距离，地月距离和月球的大小，就可以测出太阳的大小，方法和上面的差不多。

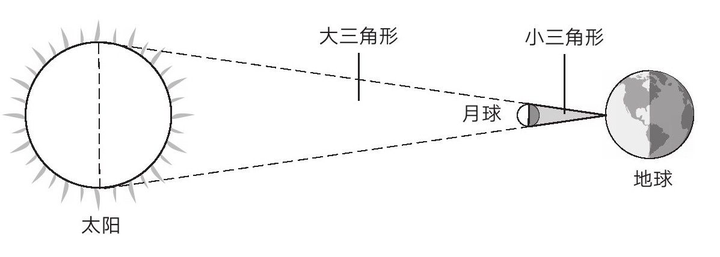
在日食发生的时候，月球几乎刚好完全遮挡太阳。利用相似三角形，就可以算出太阳的直径。

到此，地球、月球和太阳的大小，还有地日距离、地月距离都被测算出来了！

无需离开地面进入太空，也无需巨大的丈量尺，只需在好奇心的驱使下，寻找发现种种线索，再运用科学逻辑将这些线索联系起来，就能破解世界的秘密，这真是人类智慧的伟大胜利。