三维空间有莫比乌斯环,四维空间有克莱因瓶,五维六维有什么?

高维复杂得多,因为可以粘合的方向变多了,没那么好推广。
莫比乌斯环和克莱因瓶都是二维不可定向流形,一维和三维不存在不可定向流形,所以要思考四维不可定向流形的更高维嵌入,这就烧脑了。
而且做拓扑的应该都知道,四维是特殊的,哪怕更高维度都没四维复杂。
所谓不可定向,可以简单理解为绕了一圈,左右手互换了。
考虑二维平面,其实存在三种粘合方式:
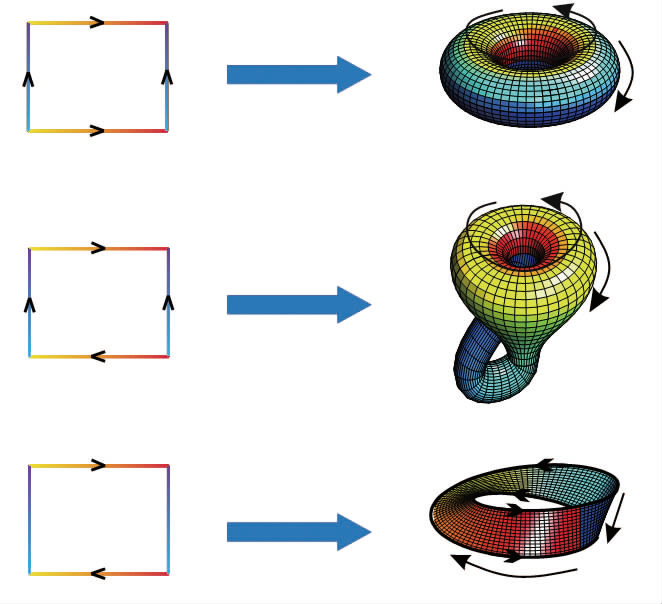
考虑一条纸带,同向粘合就是圆柱,反向粘合就是莫比乌斯环。
考虑一个圆柱,同向粘合就是甜甜圈,反向粘合就是克莱因瓶。
你比较聪明的话就会在这里发现一个 bug,那莫比乌斯环两条边不也可以正向或者反向粘合吗?
这不还有两类吗?
Sorry,莫比乌斯环只有一条边,你可以自己粘一个,真的只有一条边,没法再粘合。
所以才说二维有三种粘合方式。
总之面对高维空间几何直观已经不够用了,我们必须使用严格的数学语言来推导。
想象一条无限大的矩形纸带
,定义操作
。
在该变换下我们将所有能通过这个平移操作联系起来的点视为同一个点。
相当于把纸带卷起来,得到一个无限长的圆柱面,这仍是一个可定向的曲面。
再规定一个扭曲操作
,该变换把纵坐标翻转了,这个翻转在代数上等价一个反射操作,正是它向空间中注入了不可定向的性质。
这种特殊翻转推广到更高维度被称为对径映射(Antipodal Map)。
想象一个
维球面
,它是
空间中的单位球面。
对径映射可以把球面上的每一个点
瞬间移动到它正对面的那个点
。
打个比方,地球上的北极点和南极点建了个传送门互通,这就是一种对径映射。
这个操作可以用一个只有两个元素的群
来描述,其中
是单位操作,
是对径映射。
现在考虑一个非常抽象的粘合操作,把
上所有互为对径的点都视为同一个点,这个操作得到的商空间,就是实射影空间
。
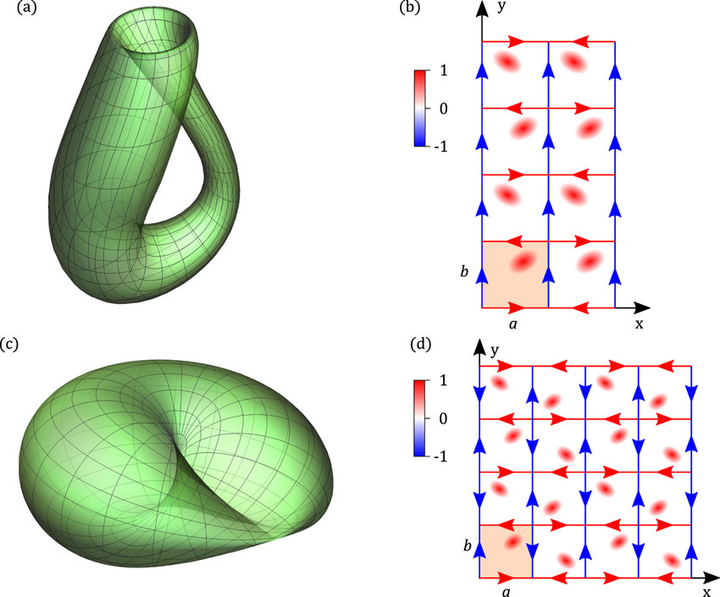
这玩意儿比克莱因瓶还要抽象一点。
就是将一维圆环
的对径点粘合,粘合后得到的还是一个圆。
所以
,并且仍然是可定向的。
要将二维球面
的对径点粘合,得到的就是上图的抽象玩意儿,这是一个二维不可定向流形,没有边界。
它和克莱因瓶是同类,都是二维紧致不可定向流形,只是在拓扑上不等同。
要将位于四维空间
中的三维球面
的对径点粘合。
这是一个三维流形,奇妙的是这个流形在拓扑上等同于我们熟知的三维旋转群
。
因此它是可定向的。
继续计算高维推广,惠特尼发现实射影空间
仅在偶数维度不可定向。
另外惠特尼强嵌入定理还指出,任何一个
维流形,无论是否可定向,总可以被嵌入到
中。
所以我们要考虑的推广就是
的
嵌入。
不过四维是被诅咒的维度,这里面水太深了。
二维世界很乖,任何紧致无边界的二维流形,要么是可定向的,要么是不可定向的,可以被完全分类。
三维的世界差不多被探索完了,任何紧致的三维流形都可以通过切割和分解,最终得到由八种标准几何结构中的一种所支配的流形块的连通和。
五维以上的世界也是井然有序,早已被微分拓扑征服。
但是四维空间上流形的分类问题异常困难,而且搞不好是不可判定的。
我随便构造一些妙妙屋。
取一个位于
中的四维球面
,然后将每一对对径点粘合在一起,得到
,这东西的嵌入需要
。
但是如果取一个二维不可定向的克莱因瓶
和一个二维可定向二维球面
,想象一个克莱因瓶,每一个点上都“挂”着一个完整的二维球面。
一个
维流形
和一个
维流形
的乘积
可以嵌入到各自嵌入空间的和中。
既然克莱因瓶
嵌入
,而球面
嵌入
,那么
可以嵌入到 7 维空间
。
这还没完,在两者身上各自挖掉一个小小的四维球体,在每个流形上下一个三维球面
作为伤口,然后将这两个三维球面的边界对齐粘合起来,串成一个高维糖葫芦
。
这东西也是不可定向的,应该需要 8 维空间
才能嵌入,长成这样我也不是很确定。
而且还能继续使用类似手段杂交下去。
总之似乎有无限种拓扑不同构的四维不可定向流形,外加一般需要八维空间才能嵌入,克莱因瓶的推广困难重重。