怎样测量天体的质量?

说个知识点:牛顿从没写过高中教材中的那个万有引力公式,也算不出太阳的质量。
以下所有内容,不超出高中一年级知识,请放心阅读。(这个问题不得不写公式,但我尽量少写公式多讲故事)
用万有引力来计算地球的重量
怎样知道天体的质量?我们举个例子,先从脚下的地球说起吧。
直到 18 世纪,科学家还测不出太阳的质量,甚至连脚下地球的质量都不知道。著名英国天文学家埃德蒙·哈雷(就是哈雷彗星的那个哈雷)甚至认为地球是空心的。
1687 年,牛顿发表了他的巨著《原理》。与高中教材中说的“假定地球公转轨道是圆的”开始用
推导出万有引力公式不同的是,他其实是从开普勒三大猜想出发(是牛顿认同其所说的地球公转轨道是一个椭圆),用平面几何(而非微积分)的方法,推导出万有引力 F 与
成正比[1]。(具体的证明过程就像高中奥数中最难的几何题一样难懂[2])
还记得高中物理老师教的万有引力公式怎么写么?
(嗯,这里有一个万有引力常数 G。事实上牛顿并没有写出这个含有 G 的公式。G 直到二个世纪后的 1873 年才第一次出现[3],这个是后话了)。
而我们假设在地表处,重力 mg 和万有引力相等(忽略自转等因素),代入上式,可以得出
这里面就有地球的质量 M 了。怎么算出来呢?这里重力加速度 g 已经被伽利略搞定了,地球半径 R 也被前人测出来了(具体测法的历史有机会我单独写一篇),那么 GM 的值就知道了,大约是
。如果我们知道 G 是多少,那就能知道地球的质量了。
但是 G 是个很难测量的值,要等到 1797 年卡文迪许用那套扭秤装置巧妙测得地球密度后,才有可能间接的求出来(与高中物理老师讲的不同的是,卡文迪许可能根本就没算过 G 的数值,而是在计算中直接消掉了)
比卡文迪许早一个世纪的牛顿并不知道引力常量 G 的值是多少。理论上,按照他自己的公式,只要测出两个物体的质量和距离,再测出它们间的引力,就能算出这个常量。我们现在高中课本上用的 G 值是约
,直接写出来就是 0.0000000000667,这是一个很小很小的数,在牛顿的那个时代,测量精度很差,如果物体的质量不大,它们间的引力就会小到无法测出。
身边什么东西质量足够大?
所以要找一个质量足够大且质量已知的物体,就能完成这个实验了。
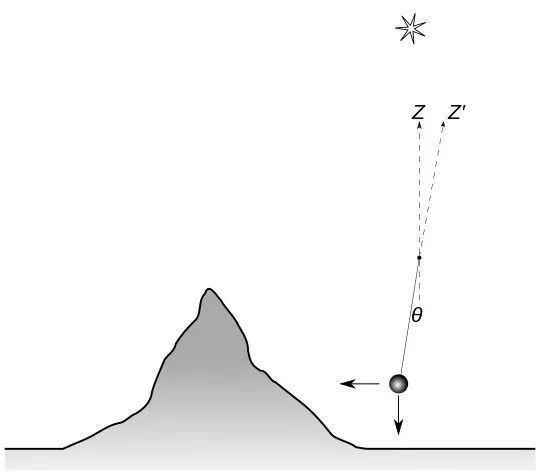
牛顿本人曾设想过找一座很大的大山,在大山的旁边放上一个单摆,摆锤会受到三种力的影响:来自大山的引力、来自地球的引力,以及绳子的张力,大山和地球对摆锤的引力的合力应该等于绳子上的拉力,而原本应竖直垂下的摆锤会因大山的万有引力而朝向大山的方向偏一个很小的角度。所以只要测算出这座山的质量,再量出摆锤偏转的角度θ,就可以计算出地球的质量。
不过,后来牛顿认为即使是质量很大的大山,让摆锤产生的偏转角也会小到几乎无法测量,更何况如何才能知道不规则形状的大山的质量?没有那么大的秤啊。这个实验没有可操作性。
所以牛顿至死也无法知道地球到底有多重。
1774 年,英国皇家天文学家内维尔·马斯基林 ( Nevil Maskelyne )却认为牛顿的想法可以实现。首先他解决了大山质量的难题。他挑选了苏格兰的一座锥形且相当对称的希哈利恩山,很容易用圆锥体公式估算出它的体积(由其测量员查理斯•赫顿计算),通过勘测岩石的密度就能计算出它的总质量。

另一方面,他借助恒星为参考点,反向延长铅锤所对应的天空恒星,从而测量出了摆锤极微小的偏转角。
最终,马斯基林团队计算出地球的平均密度为 4.5 克每立方厘米(现在各国教材通用的值是 5.5 克每立方厘米,主要误差是出在测量员低级的计算失误和采样不完备上),而希哈利恩山的平均密度只有 2.5 克每立方厘米,所以地球内部肯定有比山要重得多的物质(也就是说地球不可能是空心的)。虽然这个数值与 23 年后卡文迪许测的数值相差了近 20%,但人们终于知道地球的大概的密度了,乘上体积,就能算出地球质量了。
后来卡文迪许的扭秤实验大家都在高中教材中学过了,这里略了。
目前借万有引力测得的地球质量约为 5.965×10²⁴千克。
太阳的质量
接下来就好办了。通过卡文迪许的扭秤实验我们能得到常数 G 的值,就可以算太阳的质量了。
怎么算呢?设太阳质量为 M,某行星质量为 m,公转周期为 T,公转半径为 r。我们将行星轨道近似为圆,万有引力提供公转向心力,则有
推导出:
这个实际上就是开普勒第三定律的内容:各行星绕太阳公转周期的平方与公转轨道半径的三次方的比值 K 是与太阳质量有关的恒量。
OK,这个公式里除了太阳质量以外都是已知的,求太阳质量就变成小学数学问题了。这样算出来的太阳质量约为
千克。
太阳系其它行星的质量
那怎么求其它行星的质量呢?上面的那个公式里,只有太阳的质量,行星的质量 m 已经被左右消掉了。我们又不能去每个行星上测密度。
事实上,像火星、木星、土星这样有卫星的行星来说,可以把母星看做上面公式中的太阳 M,把卫星看做行星 m。通过望远镜观测卫星的运行周期和轨道半径,即可算出各大行星的质量(实际运算中还要考虑其它星体的影响并做修正)。当然,像月球这样质量相对较大的卫星来说,可以将地月看成一个整体,通过上面的公式算出系统总质量,再减去地球质量即可得到月球质量。
而像水星金星这样没有卫星的天体,质量就比较难求,之前只能通过光学观测测定其组成成分,再估算出密度从而求质量。现在嘛,可以发射一颗人造探测器当成其卫星,就能很方便的把它变成有卫星的行星的质量计算了。
系外星体
上面讲的套路,就是先从地球入手,再算得太阳系内其它行星和卫星。那太阳系以外呢?我们现在的天文观测结果中绝大部分是恒星,太阳系外行星的观测,对现阶段的科技水平来说还是太困难了,勉强能通过凌日(行星经过恒星时造成的光强下降)算得周期 T 就已经很好了,公转轨道半径 r 很难准确测算。怎么办?
这时候就得新工具入场了。它就是:质光关系(mass-luminosity relation)。
头都大了,怎么又出来一个新概念?好吧,从这一段开始,可能需要高三的知识了。
1912 年,两名天文学家 Ejnar Hertzsprung 和 Henry Norris Russell 分别独立发现了一个特别的现象,90%恒星的温度(颜色)和它的绝对亮度之间存在惊人的相关性。这个亮度与温度的图被称为 Hertzsprung-Russell 图,简称 H-R 图。
那质光关系又是什么?简单的说,就是质量越大的恒星,发光能力也越高。
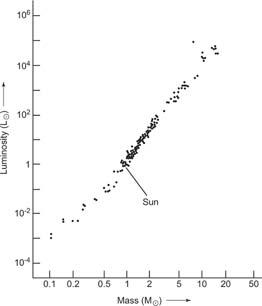
为什么呢?主序星必须通过核聚变产生的能量来提供流体静力学平衡,或者通俗的说,就是由稠密气体组成的恒星要靠核反应向外辐射的"推力"来维持其外表面,就像吹气球一样,使其不会因重力而向内坍塌。恒星质量越大意味着外表面引力的向内拉力越大(这反过来又压缩了气体,但不足以抵抗引力),从而需要更高的核反应压力来保持其平衡。而恒星内部的压力越高,温度也会越高(所以比太阳质量更大的恒星的核心温度要明显高于太阳)。在更高的温度下,核聚变反应产生能量的速度就会更快,发光能力就更强,(加上质量更高的主序星有更大半径)所以看上去就更亮。这就解释了 H-R 图相关性的谜团(不要把 H-R 图和质光关系图搞混了)。
对主序星来说,发光能力约和质量的 3.5 次方[4]成正比:
这里肯定会有人提出疑问:不对呀,我们物理老师说是 4 次方啊,这里怎么是 3.5 次方呢?当你去查百度“质光关系”时,人格分裂的度娘一会儿说是 4 次方,一会儿说是 3.5 次方[5]。事实上,这个幂是个经验值,对于近似太阳的恒星来说大约是 4,对于质量更大的恒星来说大约是 3,对于红巨星来说只有约 2.5。
综上,我们可以根据观测到的恒星的光度和光谱,来估算其质量。当然,除了用亮度来估算恒星质量外,还有其它比如维里定理[6]等方法来估计其质量,大同小异。
最难的问题
有人问,那彗星呢?怎么知道彗星的质量?
事实是,我们并不能准确测得彗星的质量,只能靠在太阳附近的挥发物光谱来做很粗的估计。除非像欧空局的罗塞塔号彗星探测器那样,直接怼一个“菲莱”着陆器到彗星 67P[7]上,测得其质量为(9.982±0.003)×10^12 千克[8][9],是登陆前估计的质量 3.14×10^12 千克[10]千克的三倍多。

还有什么感兴趣的天体?先写到这里吧,估计不会有人看到这儿的。如果你能看到这行字,请点个赞吧,谢谢了。