偶然刷到这个问题，特来恭喜题主。

你在洗澡时候独自悟出的「浴室猜想」与17 世纪哲学家英国大主贝克莱的观点——「贝克莱悖论」如出一辙！

这个悖论可是用来攻击当时刚刚创立的微积分学说的！

由于当时数学界还没有进行公理化运动，牛顿和莱布尼茨的理论并没有更深层次的关于极限的理论依据（这是后来一两百年通过魏尔斯特拉斯、康托尔、柯西、戴德金等几代数学家完成的！），所以刚出炉的微积分学遭受了业内外诸多人士的打击！

其中就包括乔治·贝克莱，著名英裔爱尔兰哲学家，同时为圣公会驻爱尔兰科克郡克洛因镇的主教，与约翰·洛克和大卫·休谟被认为是英国近代经验主义哲学家中的三大代表人物。

1734 年，大主教贝克莱以“渺小的哲学家”之名出版了一本标题很长的书《分析学家；或一篇致一位不信神数学家的论文，其中审查一下近代分析学的对象、原则及论断是不是比宗教的神秘、信仰的要点有更清晰的表达，或更明显的推理》。

在这本书中，贝克莱对牛顿的理论进行了攻击。例如他指责牛顿，为计算比如说 x²的导数，先将取一个不为 0 的增量Δx，由(x + Δx)² − x²，得到 2xΔx + (Δx)² ，后再被Δx 除，得到 2x + Δx，最后突然令Δx = 0 ，求得导数为 2x 。这是“依靠双重错误得到了不科学却正确的结果”。

因为无穷小量在牛顿的理论中一会儿说是零，一会儿又说不是零。因此，贝克莱嘲笑无穷小量是“已死量的幽灵”。

数学史上把贝克莱的问题称之为「贝克莱悖论」。笼统地说，贝克莱悖论可以表述为“无穷小量究竟是否为 0”的问题：就无穷小量在当时实际应用而言，它必须既是 0，又不是 0。但从形式逻辑而言，这无疑是一个矛盾。

这个悖论就是造成第二次数学危机的主要论题之一！而题主洗澡的时候居然独自悟出来了，如果你能穿越回过去，势必会成为时代的弄潮儿！佩服佩服。

你这个「浴室猜想」就当时而言是无人能击败的，过了一两百年才通过后代数学家的修修补补把函数、极限的理论根基定义出来。所以其他题主用十八世纪后的观点来论证嘲讽你十七世纪的观点，他们只是站在巨人的肩膀上而已，不要怕！我支持脚踏实地的题主~

穿越到十七世纪的你直到寿终正寝都不会有人辩得过你！再了解一些极限定义你就超越牛顿了，加油共勉！

这篇回答有肉眼可见的流量，就搬运一下我另一个没人看的回答吧。

我们在学校里通常是先学奠基理论（例如实数集合理论）再学高等理论。但数学史并不是这样的，往往一个划时代的全新理论并不是「踩在巨人的肩膀上」构建出来的。

我们知道实数极限的严格定义一定是建立在严格定义的实数理论和函数理论基础上的，但在微积分发明的时候，数学界并没有完备的实数、函数理论，甚至连「变量」「连续性」都没有定义。

牛顿和莱布尼兹挖了一个不见底的坑，整整一百多年，无数数学家前仆后继都在填这个坑。直至 21 世纪的今天仍有学者对这个坑不满。最后这些填上的坑却成了我们数学入门最先学习的基础理论。

「极限」是经历了第二次数学危机，微积分被严格定义后，顺带被定义下来的，由于当时实数函数理论不完备，花了几代人的时间才基本解决。

首先你得先大概了解第二次数学危机。这里直接看李永乐老师的科普视频就可以大致了解。

第二次数学危机是什么？李永乐老师告诉你阿基里斯为啥追不上乌龟？（2018 最新）_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili

然后第二次数学危机持续的 150 年里发生了什么呢？

大约在 1800 年前后，数学家们开始关心分析的庞大分支在概念和证明中的不严密性^[1]：

1. 函数概念本身就是不清楚的；
2. 使用级数而不考虑它们的收敛和发散已经产生了悖论和不同意见的争论；
3. 关于用三角级数来表示函数的论战进一步引起了混乱；
4. 导数和积分的基本概念还从来没有恰当地定义过。

所有这些困难最终导致人们对分析的逻辑状况的不满。

一些数学家决心从这种混乱中整理出一套秩序出来。这个运动的开端正好是非欧几何的创立时期。一个完全不同的数学家圈子，除了高斯以外卷入了这场运动^[1]。

首先是伯纳德·波尔查诺（Bernard Bolzano），来自波希米亚的数学家、神学家、哲学家、逻辑学家、天主教祭司和反军国主义者。二分法的发明者。

作为微积分严格化的先驱。他第一个给出了连续函数的严格定义^[2]。

连续是函数的一种属性。直观上来说，连续的函数就是当输入值的变化足够小的时候，输出的变化也会随之足够小的函数。如果输入值的某种微小的变化会产生输出值的一个突然的跳跃甚至无法定义，则这个函数被称为是不连续的函数（或者说具有不连续性）。

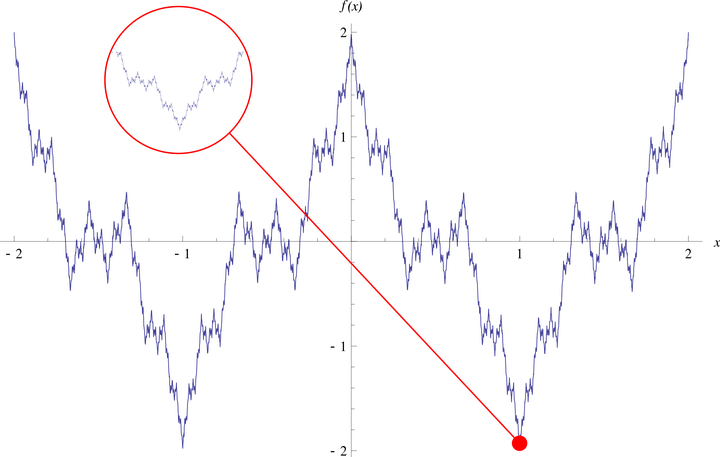
波尔查诺曾率先构造出了一种处处连续却处处不存在导数的奇怪函数^[3]。后来，魏尔斯特拉斯（Karl Weierstrass）在 1861 年^[4]也发现了类似的函数并引发轰动(但魏尔斯特拉斯直到 1874 年才将其发表^[4])，这个函数最终以魏尔斯特拉斯函数命名。波尔查诺的发现不但更早，而且只用了无穷次折线逼近的直观化方法，比魏尔斯特拉斯的方法更简单明了^[3]。

波尔查诺并不认为微积分学中常说的“无穷大量”和“无穷小量”是一种实实在在的数学量。他和伽利略一样都注意到了无穷集合可以与自身的子集建立一一对应(即希尔伯特旅馆悖论)，并都为无穷集具有这种违反直觉的性质而感到困惑和不安。

他尝试将无穷集的合理性寄托于神学论证。后来理查德·戴德金（Julius Wilhelm Richard Dedekind）则将这个新奇的性质直接作为了无限集的定义，撇开了对无穷集的哲学意义的深究。对于有关实无穷与潜无穷的哲学争论，他认为实无穷(也常译为“实无限”)是可以合理存在的。

接下来是英年早逝的挪威天才尼尔斯·亨利克·阿贝尔（Niels Henrik Abel）。群论的先驱者。

阿贝尔对“无穷级数”进行了深入研究，得到了一些重要的“判别准则”和“幂级求和”的定理，极大的推动了“分析的严格化”理论。

实数项级数的阿贝尔判别法：给定两个实数项数列

和

，如果数列满足

收敛

是单调且有界的

则级数

收敛。

阿贝尔指出，必须“严格限制”滥用“级数展开及求和”，这一思想的提出，对“第二次数学危机”的解决起到了重要作用。

然后是法国数学家奥古斯丁·路易·柯西（Augustin Louis Cauchy）。他拒绝当时微积分学的说法，并定义了一系列的微积分学准则。

在数学家对于分析的重建工作中，实数系被认为是没有任何问题的。没人企图去分析实数的结构或建立实数系的逻辑。数学家们认为他们讨论的实数问题都是立足于可靠的基础之上的。

柯西在 1821 年的《分析教程》中从定义变量出发，提出了函数的概念。

人们把依次取很多互不相同的值的量叫做变量。 当变量之间这样联系起来的时候，即给定了这些变量中一个的值，就可以决定所有其他变量的值的时候，人们通常想象这些量是用其中的一个来表达的，这时这个量就取名为自变量，而由这自变量表示的其他量就叫做这个自变量的函数。 无穷级数是规定函数的一种方法，但对函数来说不一定要有解析表达式。

和前文的波尔查诺一样，柯西也抓住了极限和连续性的概念，认为极限概念是基于纯算数的考虑：

当一个变量逐次所取的值无限趋近一个定值，最终使变量的值和该定值之差要多小就多小，这个定值就叫做所有其他值的极限。例如，一个无理数就是哪些在数值上愈来愈接近于它的不同分数的极限^[5]。

在说及函数的连续性时，柯西认为必须要说明无穷小量的主要性质：

当一个变量的数值这样地无限减小，使之收敛到极限 0，那么人们就说这个变量成为无穷小。

这样一来，柯西澄清了莱布尼兹的无穷小概念，并把无穷小量从形而上学的束缚（哲学圈的谩骂和争论）中解放了出来。

对于无穷大，柯西是这么定义的：

当变量的数值这样地无限增大，使该变量收敛到极限 ，那么该变量就成为无穷大。

于是

不再意味着是一个固定的量，而只是一个无限增大的函数变量。

接下来是函数的连续性定义：

设 是变量 的一个函数，并设对介于给定两个限「界」之间的 x 的值，这个函数总取一个有限且唯一的值。如果从包含在这两个界之间的一个 值开始，给变量 以一个无穷小增量 ，函数本身就将得到一个增量，即 ，这个差同时依赖于新变量 和原变量 的值。 假定了这一点后，如果对于每一个在这两个限中间的 的值， 的数值随着 的无限减小而无限减小。那么就说，在变量 的两限之间，函数 是变量的一个连续函数。

后来的狄利克雷（Johann Peter Gustav Lejeune Dirichlet）在柯西的理论基础上才给出了函数的现代定义。

阿贝尔在他 1826 年关于二项式的论文中赞扬柯西的成就：

每一个在数学研究中喜欢严密性的人都应该读读这本杰出的著作《分析教程》。

1823 年出版的《无穷小分析教程概论》一书内，采用和波尔查诺同样的方法定义导数，然后通过把

定义为任一有限量，把

定义为

，从而把导数的概念和莱布尼兹的微分统一起来^[1]。

对于定积分最系统的定义也是柯西开创的，并且微分和积分被顺利地整合进了同一套数学系统底下。回头翻《无穷小分析教程概论》你几乎能看到所有现代微积分基础理论的定义。

再下来就是现代分析之父——德国数学家 卡尔·魏尔施特拉斯（Karl Weierstrass）。

柯西虽然填了大部分的坑，但他著作中的严密性还是不够的。数学理论是及其严谨考究的理论，在柯西著作中充斥着“无限趋近”，“想要多小就多小”，“无穷小增量的最后比”或者“一个变量趋于它的极限”这样的不严密的描述。

魏尔施特拉斯最大的贡献就是在分析严密化方面改进了波尔查诺、阿贝尔、柯西的理论。

他攻击了“一个变量趋于它的极限”的说法，指出这种说法不幸地是人们想起时间和运动。他把一个变量简单地解释为一个字母，该字母代表它可以取值的集合中的任何一个数，这样运动就消除了。

一个连续变量是这样一个变量，如果

是该变量的值的集合中的任一值而

是任意正数，则一定有变量的其它值在区间(

,

)中。

为了消除波尔查诺和柯西在定义函数的连续性和极限中用到的短语“变为而且保持小于任意给定的量“的不明确性，魏尔施特拉斯给出了现如今所采用的定义：

如果给定任何一个正数 ，都存在一个正数 使得对于区间 内的所有 都有 ，则 在 处连续。 如果在上述说法中，用 代替 ，则说 在 处有极限 。如果函数 在区间内的每一点 处都连续，就说 在 值的这个区间上连续。

19 世纪 70 年代初，以魏尔斯特拉斯、康托尔、柯西和戴德金为代表的数学家开展了轰轰烈烈的数学公理化运动。戴德金利用戴德金分割定义了无理数和实数的概念，并且指出实数是完备（连续）的。按照戴德金分割，我们可以证明 0.999...和 1 完全相等。

0.999…=1？数到底是什么？李永乐老师讲数学公理化_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili

正是因为数学公理化运动，才使得数学有了坚实的基础。第二次数学危机也宣告结束。